ВЫБЕРИ репетитора! Промокод на скидку 25283
НОУТБУК за 16000 рублей!
|
Отзывов (7)

В состав ЕГЭ по математике включёна целая группа задач, относящаяся к задачам на движение — это задачи на движение по воде. Задачи несложные, решаются по той же формуле. Мы уже рассматривали с вами задачи на движение «Задачи на прямолинейное движение. Часть 1» и другие.  Принципы те же. Используется основная формула:

Но в задачах на движение по воде (по реке), добавляется лишь небольшое условие. Необходимо учитывать скорость течения реки. Скорость судна определяется следующим образом:

Если плыть по течению реки, то к скорости судна в неподвижной воде необходимо прибавить скорость течения.

Если плыть против течения, то из скорости судна в неподвижной воде необходимо вычесть скорость течения.

Так же необходим навык быстрого решения квадратного уравнения. На самом ЕГЭ это сэкономит ваше время. Иногда требуется извлечь корень из большого числа, по этому поводу изучите статью «Извлекаем корень из большого числа».

Рассмотрим задачи: Далее

Категория: Движение | ЕГЭ-№10
|
Отзывов нет

Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи   "Задачи на прямолинейное движение. Часть 1" и "Задачи на прямолинейное движение. Часть 2".  Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.

Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время  То есть формула средней скорости такова:

Далее

Категория: Движение | ЕГЭ-№10
|
Отзывов (2)

В этой статье мы с вами рассмотрим типовые задания, которые включены в состав экзамена по математике. При работе с ними требуются знания и навыки решения показательных уравнений и неравенств. Представленные задачи особой сложности не представляют, процесс сводится к решению простейших уравнений (неравенств). В этой рубрике нами уже были рассмотрены некоторые задачи, можете изучить статьи «Задачи с логарифмами»  и «Задачи по физике. Это не страшно!».

Вспомним свойства показателей степени:

a0= 1

Нулевая степень любого числа равна единице.

* * *

Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный.  Например: Далее

Категория: Физические задачи | ЕГЭ-№9
|
Отзывов (5)

    Здравствуйте, Дорогие друзья! Сегодня пост короткий. Небольшая новость для всех, кого интересует тема блоггинга. На днях написал книгу, конечно, звучит это громко, но в интернете подобные электронные творения называют именно так –  книга.

Далее

Категория: НОВОСТИ | РекомендацииСАМОРАЗВИТИЕ
|
Один отзыв

На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники.

Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.

Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.

Далее

Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№3
|
Отзывов (2)

В этой статье рассмотрим задачи на нахождение элементов  конуса. Конечно же, их можно отнести к одним из самых простых задач, которые входят в открытый банк заданий ЕГЭ по математике.

Как и многие задачи этой части, решаются они в одно-два действия. Несмотря на то, что это это стереометрическая задача, для решения достаточно знать теорему Пифагора. Рассмотрим задачи:

Высота конуса равна 57, а диаметр основания — 152. Найдите образующую конуса.
Рассмотрим осевое сечение конуса. По теореме Пифагора:
Категория: Стереометрия КОНУС ЦИЛИНДР | ЕГЭ-№3
|
Отзывов (3)

Знаки тригонометрических функций. Друзья! В одной из прошлых статей, где мы рассматривали решение задач на вычисление значений тригонометрических выражений, предлагалось запомнить как факт —

Знаки тригонометрических функций

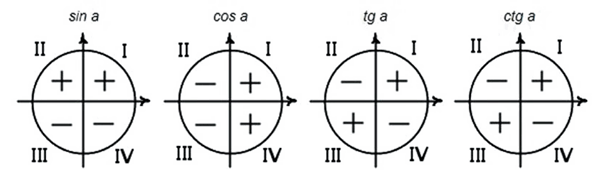
Помнить эту информацию крайне необходимо. Но необходимо понимать из чего она  исходит, так как именно понимание этого – есть одно из основных  условий усвоения сути тригонометрии.

Построим тригонометрическую окружность (окружность на координатной плоскости с радиусом равным единице); радиус-вектор, повернутый на произвольный угол от 0 до 90 градусов; обозначим абсциссу и ординату точки пересечения радиус-вектора и единичной окружности соответственно х и у: Далее

Категория: Формулы Теория | ТригонометрияФормулы