Знаки тригонометрических функций

Знаки тригонометрических функций. Друзья! В одной из прошлых статей, где мы рассматривали решение задач на вычисление значений тригонометрических выражений, предлагалось запомнить как факт —

Знаки тригонометрических функций

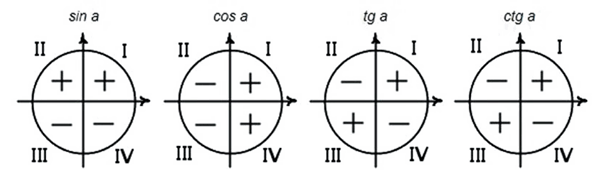
Помнить эту информацию крайне необходимо. Но необходимо понимать из чего она  исходит, так как именно понимание этого – есть одно из основных  условий усвоения сути тригонометрии.

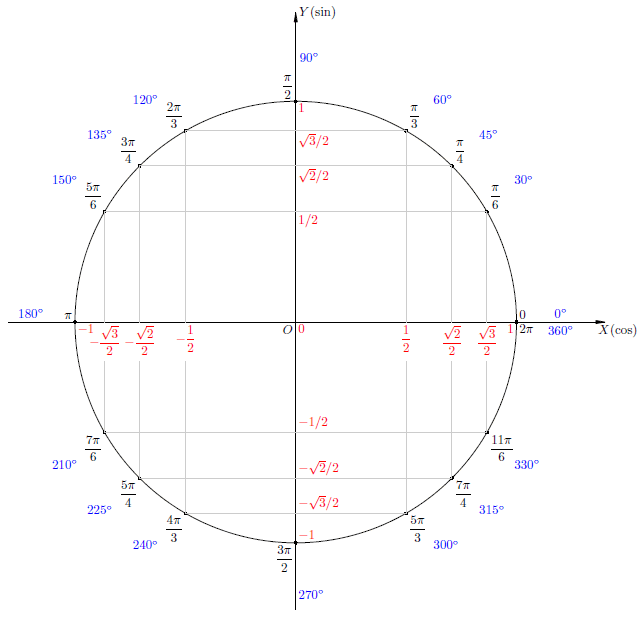
Построим тригонометрическую окружность (окружность на координатной плоскости с радиусом равным единице); радиус-вектор, повернутый на произвольный угол от 0 до 90 градусов; обозначим абсциссу и ординату точки пересечения радиус-вектора и единичной окружности соответственно х и у:

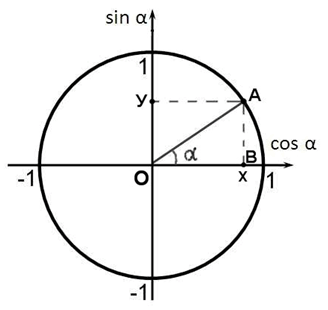
ОА – это радиус-вектор;

А – точка пересечения радиус-вектора и тригонометрической окружности;

α (альфа) – угол, на который поворачивается радиус-вектор;

у – ордината точки А;

х – абсцисса точки А;

Рассмотрим прямоугольный треугольник ОВА.

По определению синуса в прямоугольном треугольнике:

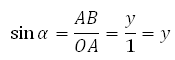
Вывод (он же является определением синуса):

Синусом угла α (альфа) называется ордината (координата y) точки на тригонометрической окружности, которая возникает при повороте радиус-вектора на угол α.

Следствие, которое можем сделать:

Значения синусов углов лежащих в первой и второй четверти  положительны, а лежащих в третьей и четвёртой четверти отрицательны.

По определению косинуса в прямоугольном треугольнике:

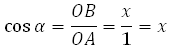
Вывод (он же является определением косинуса):

Косинусом угла α (альфа) называется абсцисса (координата x) точки на тригонометрической окружности, которая возникает при повороте радиус-вектора на угол α.

Следствие, которое можем сделать:

Значения косинусов углов лежащих в первой и четвёртой четверти  положительны, а лежащих во второй и третьей четверти отрицательны.

По определению тангенса в прямоугольном треугольнике:

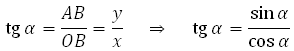
Тангенс угла α (альфа) — это отношение синуса к косинусу.

Или, по-другому — отношение координаты  y  к координате  x.

По определению котангенса в прямоугольном треугольнике:

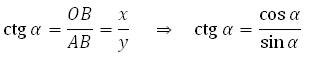
Котангенс угла α (альфа) — это отношение косинуса к синусу. 

Или, по-другому — отношение координаты  x  к координате  y.

Знаки тангенса и котангенса в четвертях определяются просто, в каждой четверти определяем знак синуса и косинуса, далее делим:

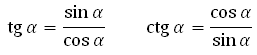
При делении положительного числа на положительное, получаем положительное число; при делении положительного числа на отрицательное получаем отрицательное число.

При делении отрицательного числа на положительное, получаем отрицательное число; при делении отрицательного числа на отрицательное получаем положительное число.

Как вы поняли, знаки тангенса и котангенса в соответствующих четвертях одинаковы.

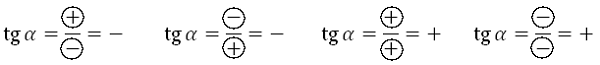
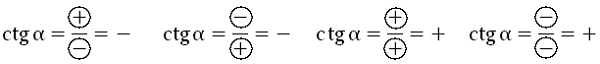
Кстати, один из выводов, который следует из определений синуса и косинуса:

Известно, что по теореме Пифагора ОА² = АВ² + ОВ², то есть 1 = у² + х²

По определению синуса и косинуса, изложенным выше:

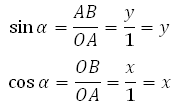
ЗНАЧИТ

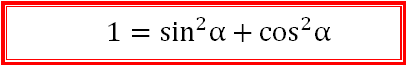
А ЭТО ЕСТЬ

ОСНОВНОЕ ТРИГОНОМЕТРИЧЕСКОЕ ТОЖДЕСТВО

Как видим, основное тригонометрическое тождество и теорема Пифагора «крепко» связаны. Понимание «природы» этой формулы, а также знание  информации, которую даёт нам тригонометрическая окружность определяет успех в изучении разделе курса «Тригонометрия» . 

Следующих определений в курсе тригонометрии не существует, это скорее «словесная связка»  или своеобразный штамп, который позволяют быстро вспомнить информацию. Излагаю только потому, что мне лично это помогало быстро вспоминать сами определения синуса и косинуса, а также знаки функций в четрвертях. Буду рад, если это поможет и вам.

Предлагаю  запомнить:

Если вы это чётко усвоите, то например, если речь пойдёт о синусе какого-либо угла, то мысленно можно проецировать точку пересечения радиус-вектора и единичной окружности на ость оу (ось ординат) и определять значение синуса этого угла (разумеется если значение табличное). Можно не мысленно, а по эскизу:

В разделе ФОРМУЛЫ мы продолжим рассматривать полезные теоретические моменты, не пропустите!

На этом закончим. Успехов вам! 

С уважением, Алексндр Крутицких.

P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.