Найдите тангенс альфа, если синус альфа

В данной статье мы с вами разберём некоторые задачи связанные с выражениями. Задания данной группы довольно разнообразны. Если вы запомнили свойства степеней, корней и логарифмов, знаете основные формулы тригонометрии, и постоянно практикуетесь, то большинство задач для вас никакого труда не представят.

Относительную сложность могут вызывать следующие:

— преобразования буквенных иррациональных выражений
— вычисление значений тригонометрических выражений
— преобразования тригонометрических выражений

Если перечислить все группы задач, то они довольно разнообразны.

Здесь мы с вами разберём задачи на вычисление значений тригонометрических выражений. Конечно, все их в одной статье разобрать невозможно. Но мы обязательно разберём и другие примеры, не пропустите!

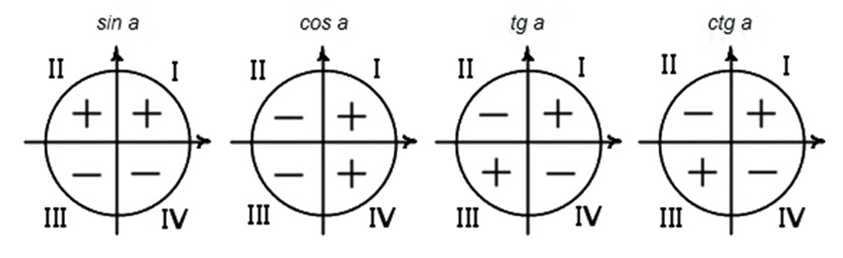
Итак, что обязательно вы должны знать и всегда помнить? Это знаки тригонометрических функций в четвертях. ЭТО ВАЖНО!!!

Как  осознать эту  информацию и понять  следствием чего она является –  об этом будет отдельная статья (если вы это знаете, то прекрасно). Пока предлагаю пока просто запомнить:

Основное тригонометрическое тождество:

Формулы тангенса и котангенса:

Выполняются элементарные алгебраические преобразования:

1. Числитель и знаменатель дроби можем умножать и делить на одно и тоже число.
2. Левую и правую часть уравнения можем умножать и делить на одно и тоже число.

В представленных ниже заданиях используется основное тригонометрическое тождество и формула тангенса.

Найдите тангенс альфа, если

В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:

Косинус угла нам известен. Из формулы основного тригонометрического тождества  мы можем найти значение синуса. Затем подставить их в формулу тангенса.

Теперь ВАЖНЫЙ момент: необходимо определить знак синуса для интервала (3Пи/2;2Пи). Это интервал от 270 до 360 градусов (четвёртая четверть).  Как переводить радианы в градусы можно посмотреть здесь. Значение синуса в этой четверти отрицательное, поэтому:

Таким образом:

Ответ: – 0,5

Найдите tg α, если

В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:

Cинус угла нам известен. Из формулы основного тригонометрического тождества  мы можем найти значение косинуса. Затем подставить их в формулу тангенса.

Определяем знак косинуса для интервала (Пи/2;Пи). Это интервал  от 90 до 180 градусов (вторая четверть). Значение косинуса в этой четверти отрицательное (смотрите эскиз). Поэтому

Таким образом:

Ответ: – 0,25

Необходимо найти косинус угла. Из формулы основного тригонометрического тождества следует, что cos²x = 1– sin²x и

Определим знак косинуса. Угол принадлежит интервалу (3Пи/2;2Пи).

Это интервал от 270 до 360 градусов  (четвёртая четверть).  Значение косинуса в этой четверти  положительное, поэтому:

Таким образом, 5·cos α = 5∙0,7 = 3,5

Ответ: 3,5

Найдите 0,1·sin α, если

Необходимо найти синус угла. Из формулы основного тригонометрического тождества следует, что sin²x = 1– cos²x  и

Определим знак синуса. Угол принадлежит интервалу (0; Пи/2).

Это интервал от 0 до 90 градусов  (первая четверть).  Значение синуса в этой четверти  положительное, поэтому:

Таким образом 0,1·sin α = 0,1∙0,3 = 0,03

Ответ: 0,03

Общая рекомендация для следующих данных примеров! Если требуется найти тангенс аргумента (квадрат  тангенса), то осуществляем деление на косинус (квадрат косинуса). Если требуется найти котангенс аргумента (квадрат  котангенса), то осуществляем деление на синус (квадрат синуса). Примеры:

65217. Найдите tg² α, если  3sin² α + 8 cos² α = 7

Требуется найти квадрат тангенса. Разделим обе части уравнения на cos² α, получим:

Второй способ:

Далее по формуле основного тригонометрического тождества можно найти квадрат синуса и используя формулу тангенса вычислить уже его квадрат:

Ответ: 0, 25

65269. Найдите

Преобразуем данное выражение так, чтобы в числителе и знаменателе был тангенс. Разделим числитель и знаменатель на cos α, получим:

Ответ: – 0,5

65273. Найдите

Здесь дано значение тангенса. Необходимо сделать так, чтобы в выражении у нас был тангенс. Вынесем cosα за скобки в числителе и знаменателе (или разделим числитель и знаменатель на  cosα), получим:

Подставим значение тангенса данное в условии, получим:

*Косинус у нас сократился.

Ответ: 4

65363. Найдите tg α, если

В левой части в числителе и знаменателе вынесем cosα за скобки, получим:

Ответ: 0,4

65423. Найдите tg α, если

Умножим обе части уравнения на  4 (2sinα+cosα+1)

Ответ: –1,9

26775. Найдите tg α, если

Посмотреть решение

26776. Найдите tg α, если

Посмотреть решение

26777. Найдите 3cos α, если

Посмотреть решение

26778. Найдите 5sin α, если

Посмотреть решение

26787. Найдите  tg² α, если

Посмотреть решение

26788. Найдите

Посмотреть решение

26789. Найдите

Посмотреть решение

26790. Найдите tg α, если

Посмотреть решение

26791. Найдите tg α, если

Посмотреть решение

Подведём итог, для решения подобных примеров вы:

1. Должны знать на зубок основные формулы тригонометрии.
2. Не забывать определять знак (+ или -) для тригонометрических функций в четвертях. Потерянный знак на экзамене – это ошибка и потерянный бал, будьте внимательны!!!

Надеюсь, что материал был для вас полезен.

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.