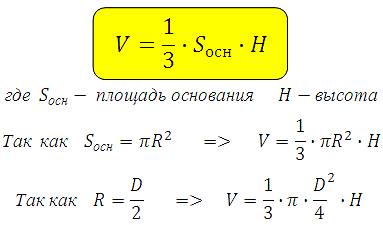Здесь для вас представлено решение двух заданий связанных с комбинацией двух тел – сферы и куба. На момент публикации этих строк данные задачи исключены из банка заданий ЕГЭ по математике, то есть их как бы на экзамене быть не должно. Но нельзя исключать такой возможности, что их в любой момент могут «вернуть» обратно. Поэтому рассмотреть их считаю обязательным.
В чём может возникнуть затруднение? В условии не дан эскиз, и сразу после прочтения не совсем понятно как выглядит указанная «конструкция». Если у вас хорошее пространственное мышление, то вы вполне можете обойтись без эскиза.
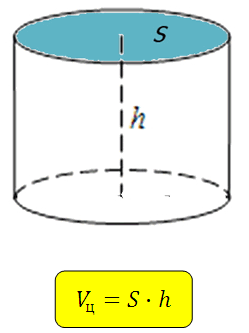
Напомню формулу площади поверхности шара, она необходима:

Как легко запомнить формулу было описано в этой статье.
Рассмотрим задачи: Далее