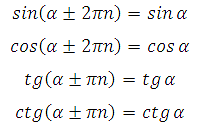Задания с которыми должен ознакомиться каждый выпускник
=> Хотите быть готовыми к коварным задачам на экзамене?
=> Желаете избежать обидных и лишних ошибок?
=> Считаете, что время важный фактор при решении?
=> Хотели бы научится решать задачи за пару минут?
=> ТОГДА ЭТА КНИГА ДЛЯ ВАС <=
Подготовка к ЕГЭ. Александр Крутицких
www.matematikalegko.ru
Здравствуйте, Дорогие друзья! Приветствую всех участников Марафона. Если сегодня вы случайно зашли на сайт и оказались на этой странице — тоже присоединяйтесь, все условия здесь.
14 сентября РОВНО в 12:00 (МСК) «проявятся» задания. Не забудьте в это время обновить страницу. Если задания не появятся, обновляйте её снова и снова, загрузка должна пройти в течении 10-15 секунд.
Окружность касается сторон угла, отношение радиусов окружностей. В этой статье разберём один теоретический момент, который может встретиться при решении задачи по геометрии. В любом случае, пусть данный материал будет в вашей «математической копилке», пригодится. Речь пойдёт о двух окружностях, которые лежат внутри угла, касаются его сторон и друг друга. Мы выведем формулу отношения их радиусов. Построим эскиз:
Найти абсциссу точки. Друзья! В этой статье для вас размещено ещё несколько заданий связанных с координатной плоскостью. Решение данного типа задач, входящих в состав ЕГЭ очень простенькое – решаются они практически сходу в течение минуты. Если вы забыли, что такое абсцисса и ордината, то посмотрите эту статью.
Суть рассматриваемых ниже задач такая – даны фигуры на плоскости, заданы координаты вершин (не всех), необходимо определить абсциссу или ординату неизвестной вершины. Также имеются задачи на определение длины отрезка. Если у вас развито визуальное (зрительное) представление, то решение вы «увидите» сразу посмотрев на эскиз.
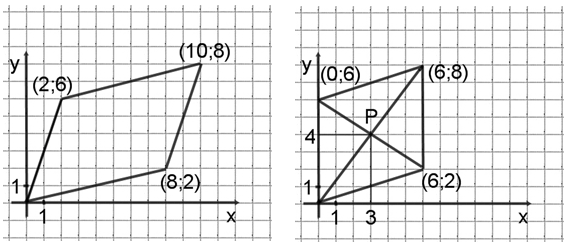
Если есть сложности с визуальным представлением фигур на координатной плоскости, то моя вам «универсальная» рекомендация – постройте фигуру по данным координатам на листе в клетку, далее вы без труда определите координаты (местонахождение) вершины или оговоренной в условии точки и ответите на поставленный вопрос. Посмотрите, как это будет выглядеть такое построение:
Вычисление значений тригонометрических выражений. В этой статье мы рассмотрим несколько примеров на вычисление значений тригонометрических выражений. В одной из статей уже были представлены такие примеры, посмотрите. Что необходимо знать, понимать и уметь применять?
Это формулы приведения, формулы периодичности тригонометрических функций, чётность нечётность, знаки тригонометрических функций в четвертях тригонометрической окружности, и конечно же, как всегда, требуется внимательность при вычислениях.
Периодичность тригонометрических функций.
Подробно саму теорию о периодичности здесь разъяснять не стану, будет отдельная статья, напомню вам только сами формулы:
Здравствуйте, Дорогие друзья! В прошлой статье, где говорил о изменениях ЕГЭ 2015, я обмолвился о том, что буду ежемесячно проводить онлайн-марафон по решению задач. Цель простая — конкурсы это всегда интересно и элемент состязательности он как-то оживляет атмосферу. Получил несколько вопросов на тему: Как это будет проходить? Какие будут призы? Какие будут задания? И прочее. Решил написать отдельную статью и разложить всё по полочкам.
Здравствуйте, Дорогие друзья! Вот и наступил сентябрь, а с ним, конечно же, новый учебный год. Желаю вам неуёмной энергии в изучении новых знаний, сил, чтобы информация легко усваивалась. Успеха вам в делах и добрых отношений со сверстниками. Уважаемые педагоги, Вам здоровья, мудрости и благополучия в семье!
Пусть кто-то говорит, что современная система образования в школах далека от совершенства, но нельзя отрицать факт того, что педагоги прививают мега ценную привычку — учиться и познавать. Не все эту привычку перенимают, но это уже другой разговор.
Лечение остеохондроза в домашних условиях. Не поспоришь — много сидим, мало двигаемся, зарядку не делаем, восстанавливать позвоночник и снимать мышечное напряжение не умеем — все нам некогда ... И он, тут как тут, этот самый остеохондроз.
Несмотря на то, что в области медицины наблюдается интенсивное развитие, многие болезни значительно помолодели. К ним стоит отнести не только остеохондроз, гипертонию, артроз, сахарный диабет и прочие. Еще не так давно эти заболевания были присущи людям старшего возраста, а сегодня их все чаще диагностируют у молодых людей и даже детей. Далее
