![]()
Формулы приведения! Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
*А тем, кто хочет набить руку решая задачи, вот здесь разобраны 22 примера от простых до самых сложных.
Перечислю лишь некоторые задачи, типы которых возможны на экзамене, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
Формулы приведения:
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:

функция изменяется на кофункцию

функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:

![]() Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов, значит:
Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:

Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
![]() Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение прямоугольного треугольника был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения:
Конечно, определить значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.
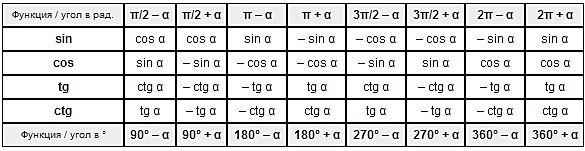
Данные формулы можно также выразить в табличной форме:
В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 10500, -7500, 23700 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!
Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию. На этом всё. Надеюсь, материал был вам полезен.
Получить материал статьи в формате PDF
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.








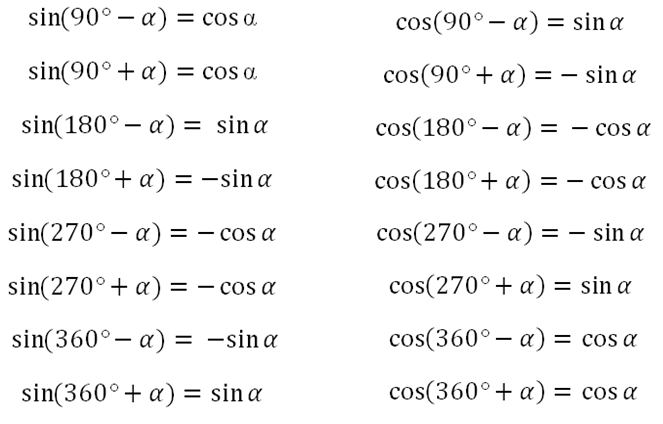





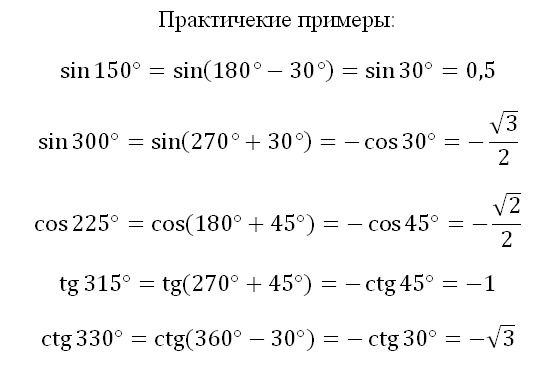








Спасибо.
Спасибо огромное за Ваш труд! Замечательный сайт! Очень много полезной, нужной информации!!!
Пожалуйста! 😉
Спасибо, я бы хотела узнать о прикладных сторонах формул приведения. В жизне как используется?
При расчётах — проектировка механизмов, устройств, приборов. При расчётах, например, при раскройке мебельных листов ДСП, которые используются для изготовления мебели. Обычным людям в повседневной жизни они как бы не нужны.
Объясните пожалуйста как в первом практическом примере взялось 180°-30°?
Нам необходимо 150 представить (подвести) в той форме, чтобы было возможно применить формулы приведения. Я взял 180-30, можно было написать 90+60, это не важно, результат всё-равно будет один. Есть вопросы, пишите...
Cпасибо большое, наконец то доча с помощью вашего объяснения поняла тему, настолько все объяснено просто и доступно!
Спасибо большое за статью,все понятно,теперь не надо учить формулы,
Александр Крутицких спасибо вам! Всё понятно и доходчиво написано,еще раз огромное спасибо.
класс!!!
Автор, вы просто молодец, я очень вам благодарен.
Благодаря вам я наверстал упущенное!
Рад! 😉 Прилашаю
http://matematikalegko.ru/konkursi-na-matematikalegko/onlajn-marafon-zarabotaj-na-reshenii-zadach.html
Объясните,пожалуйста,почему в одном задании угол 180 градусов лежит во второй четверти,а в другом в третьей?
И вообще,я не понимаю как определять четверти,хотя это легко,но я не могу понять,почему,например угол в 90 градусов лежит во второй четверти?
Владислава, посмотрите как расположены четверти
matematikalegko.ru/formul...kix-funkcij.html
Изучите эту статью обязательно.
Углы 90, 180, 270, 360 являются границами четвертей. А вот угол 90-а уже лежит в четверти (в первой). Как определяется знак функции посмотрите в указанной статье.
Вот ещё
ege-study.ru/formuly-privedeniya/
Извините , не объясните , пожалуйста , в чем моя ошибка ?
sin (90 + a) = cosа . Данный угол лежит во второй четверти . Cos во второй четверти отрицательный . Так почему тогда в формуле нету знака минус перед cosa?
Николай, здравствуйте!
Мы рассматриваем функцию синуса угла во второй четверти. ИМЕННО синус во второй четверти положителен, потому и + перед косинусом. То есть оценивается начальная функция (от которой исходим).
То есть можно говорить об универсальном правиле без запоминания формул приведения :
Через П и 2П — функция не меняется, а знак в зависимости от четверти .
Через П\2 и 3П\2 функция меняется на кофункцию , при этом знак остается от изначальной функции ?
Почти )
С изменением функции на кофункцию всё верно. А знак зависит только от четверти исходной функции.
Через П\2 и 3П\2 функция меняется на кофункцию , при этом знак также в зависимости от четверти.
Например
ctg (3Пи/2-а)=tg a
Так как 3Пи/2, то функция меняется на кофункцию.
Так как котангенс в третьей четверти положителен, то знак +.
Все понятно . Спасибо большое за объяснение )
Как преобразовать формулу четырёх угольника ?
В четырёхугольной произвольной призме
Спасибо Вам огромное! Все предельно просто и ясно изложено!
Здравствуйте!
Как привести к наименьшему положительному аргументу:
sin2000°,cos (-2900°),tg606°,ctg1315°,sin (-7,3π),ctg (-41/45π),tg (-17/18π),cos34/9π
Здравствуйте, Амина. Двумя словами не расскажешь. Используйте понятие периода, чётности нечётности.
СПАСИБО ОГРОМНОЕ, ВСЕГО ХОРОШЕГО!!!
а как определять формулы приведения на тригонометрическом окружности
Спасибо, всё просто и ясно, думал вообще никогда не пойму, а благодаря вашему материалу разобрался за 5 минут! Порадовал тренажёр для закрепления в конце, но хотелось бы больше примеров в нём!
Очень полезная статья! Хотела бы уточнить к каким четвертям принадлежат углы в 90, 180, 270 и 360 градусов. Спасибо!
Они являются границами четвертей. Функции синуса и косинуса этих углов легко определяются по тригонометрической окружности, а тангенса и котангенса по формулам отношения синуса и косинуса.
спасибо, очень помогло!)
Здравствуйте, как привести в подобном случае?
Привести sin 253° к значению тригонометрической функции положительного аргумента, меньшего 45°.
Только с помощью формул приведения не привести. Тут задачка посложнее будет. Посмотрю ...