![]()
Мы уже разобрали с вами почти все типы заданий входящих в ЕГЭ связанных с координатной плоскостью, рекомендую посмотреть последнюю статью. Эта является её небольшим дополнением, принципы и подходы к решению те же. Рассмотрим задачи:

27693 (94). Какого радиуса должна быть окружность с центром в точке P (8;6), чтобы она касалась:
1. Оси абсцисс?
2. Оси ординат?
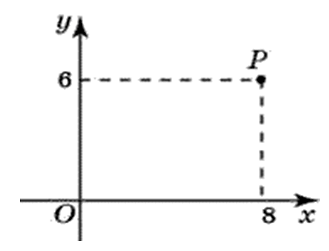
Окружность с центром в точке Р будет касаться оси абсцисс в точке с координатами (8;0) и её радиус будет равен шести (на эскизе изображена синим цветом).
Окружность с центром в точке Р будет касаться оси ординат в точке с координатами (0;6) и её радиус будет равен восьми (на эскизе изображена красным цветом).


27696 (97). Найдите абсциссу и ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (–2;–2), (6;–2), (6;4), (–2;4).

Как известно, точка пересечения диагоналей прямоугольника и центр описанной около него окружности совпадают. *По свойству прямоугольника его центр равноудалён от его вершин и сторон.
То есть необходимо определить абсциссу и ординату точки пересечения диагоналей прямоугольника. Сделать это можно разными способами:
1. Найти координаты середины отрезка АС (или CD) по формуле.
2. Построить прямоугольник по данным координатам на листе в клетку, вместе с его диагоналями.
Воспользуемся вторым способом:

По эскизу видно, что центр прямоугольника имеет координаты (2;1). Таким образом, абсцисса центра окружности равна двум, а ордината равна единице.

27699 (700). Найдите абсциссу и ординату центра окружности, описанной около треугольника, вершины которого имеют координаты (8;0), (0;6), (8;6).

Данный треугольник является прямоугольным. О прямоугольном треугольнике и описанной около него окружности нам известно следующее:
Гипотенуза прямоугольного треугольника и диаметр описанной около него окружности совпадают.
Подробнее об этом изложено здесь (пункт 1).
*Данное свойство рекомендую запомнить раз и навсегда, пригодится при решении многих заданий.
Так как АВ является диаметром окружности, то её центр делит этот отрезок пополам. Опытный глаз сразу «увидит», что координаты этой точки (4;3).

Если не увидели, то постройте этот треугольник на листе в клетку по данным координатам и далее вы без труда определите как расположен центр окружности. Абсцисса равна четырём, ордината равна трём.
![]()
27692. Окружность с центром в начале координат проходит через точку P (8;6). Найдите ее радиус.

27695. Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (–2;–2), (6; –2), (6; 4), (–2; 4).

27698. Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8;0), (0;6), (8;6).

На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.















