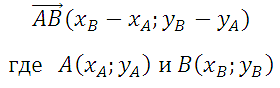Скалярное произведение векторов (далее в тексте СП). Дорогие друзья! В состав экзамена по математике входит группа задач на решение векторов. Некоторые задачи мы уже рассмотрели. Можете посмотреть их в категории «Векторы». В целом, теория векторов несложная, главное последовательно её изучить. Вычисления и действия с векторами в школьном курсе математики просты, формулы не сложные. Загляните в справочник. В этой статье мы разберём задачи на СП векторов (входят в ЕГЭ). Теперь «погружение» в теорию:
Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты его начала

И ещё: