Длина отрезка. Середина отрезка

Длина отрезка. Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые  решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).

Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой. Большинству эти задания будут не интересны. Но изложить их считаю необходимым.

Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь немного теории.

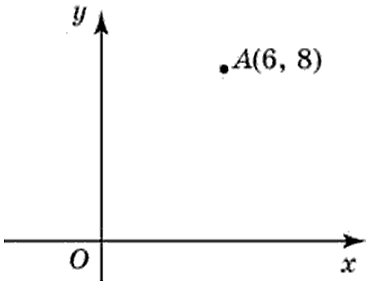
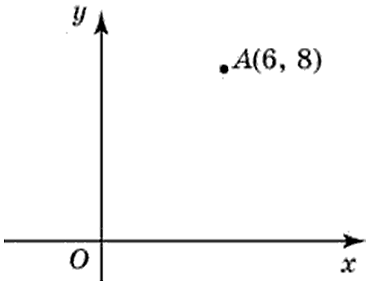
Построим на координатной плоскости точку А с координатами х= 6, y=3.

Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.

Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.

То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.

Длина отрезка на координатной плоскости

Формула для определения длины отрезка, если известны координаты его концов:

Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными

Х_В – Х_А     и    У_В – У_А     

* * *

Середина отрезка. Её Координаты.

Формула для нахождения координат середины отрезка:

Уравнение прямой проходящей через две данные точки

Формула уравнения прямой походящей через две данные точки имеет вид:

где  (х₁;у₁) и (х₂;у₂)  координаты заданных точек.     

Подставив значения координат в формулу, она приводится к виду:

y = kx + b, где k — это угловой коэффициент прямой

Эта информация нам понадобиться  при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!

Что ещё можно добавить?

Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.

Рассмотрим задачи.

Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.

Основание перпендикуляра опущенного на ось ординат будет иметь координаты  (0;8). Ордината равна восьми.

Ответ: 8

Найдите расстояние от точки A с координатами (6;8) до оси ординат.

Расстояние от точки А до оси ординат равно абсциссе точки А.

Ответ: 6.

Найдите ординату точки, симметричной точке A(6;8) относительно оси Ox.

Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).

Ордината равна минус восьми.

Ответ: – 8

Найдите ординату точки, симметричной точке A(6;8) относительно начала координат.

Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).

Её ордината равна  – 8.

Ответ: –8

Найдите абсциссу середины отрезка, соединяющего точки O (0;0) и A(6;8).

Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).

Вычисляем по формуле:

Получили (3;4). Абсцисса равна трём.

Ответ: 3

*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.

Найдите абсциссу середины отрезка, соединяющего точки A(6;8) и B(–2;2).

Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).

Вычисляем по формуле:

Получили (2;5). Абсцисса равна двум.

Ответ: 2

*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.

Найдите длину отрезка, соединяющего точки (0;0) и (6;8).

Длина отрезка при данных координатах его концов вычисляется по формуле:

в нашем случае имеем О(0;0) и А(6;8). Значит,

*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:

Ответ:10

Найдите косинус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.

Угол наклона отрезка – это угол между этим отрезком и осью оХ.

Из точки А опустим перпендикуляр на ось оХ:

То есть, угол наклона отрезка это  угол ВОА в прямоугольном треугольнике АВО.

Косинусом острого угла в прямоугольном треугольнике является

отношение прилежащего катета к гипотенузе

Необходимо найти гипотенузу ОА.

По теореме Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Таким образом, косинус угла наклона равен 0,6

Ответ: 0,6

Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.

Посмотреть решение

Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ.

Посмотреть решение

Найдите расстояние от точки A с координатами (6;8) до оси абсцисс.

Посмотреть решение

Найдите расстояние от точки A с координатами (6;8) до начала координат.

Посмотреть решение

Найдите абсциссу точки, симметричной точке A(6,8) относительно оси оУ.

Посмотреть решение

Найдите абсциссу точки, симметричной точке A(6,8) относительно начала координат.

Посмотреть решение

Найдите ординату середины отрезка, соединяющего точки O (0;0) и A (6;8).

Посмотреть решение

Найдите ординату середины отрезка, соединяющего точки A (6;8) и B (-2;2).

Посмотреть решение

Найдите ординату точки пересечения оси оУ и отрезка, соединяющего точки A (6;8) и B (- 6;0).

Посмотреть решение

 Найдите длину отрезка, соединяющего точки А(6;8) и В(-2;2).

Посмотреть решение

Найдите синус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс. 

Посмотреть решение

Это даже не задача, а вопрос. 

Частенько Александр Васильевич Суворов, встречая любого подчинённого, который случайно попадался ему на глаза задавал вопрос, порой неожиданный. Однажды спросил офицера своей армии:"Сколько вёрст до луны?". Что тот ответил?

Первый, кто даст правильный ответ получит поощрительный приз — 100 рублей. Ответы пишите в комментариях.

На этом всё. Успехов вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.