![]()
Здравствуйте! В этой статье речь пойдёт о задачах, которые можно решать без нахождения производной. В данной рубрике мы уже рассмотрели некоторые примеры с логарифмами, числом е, функции с произведениями. Смысл заданий тот же – требуется найти либо точку максимума (минимума) функции, либо определить максимальное (минимальное) значение функции.
В чём суть и каков «стандартный» алгоритм решения — можно посмотреть в этой статье. Но не для всех заданий применение этого алгоритма будет рационально. Если следовать ему в представленных ниже примерах, то процесс решения будет «перегружен» вычислениями. А потеря времени на экзамене вам не нужна. Так какие же задания имеются ввиду?
В условии дана иррациональная, логарифмическая или показательная функция:
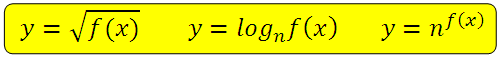
при чём под корнем, под знаком логарифма или в показателе находится квадратичная функция вида:

Рассмотрим подход без нахождения производной. Вы увидите, что такие задачи можно решать устно.
Что необходимо знать? Свойство параболы, напомним его:
Если а > 0, то её ветви направлены вверх.
Если а < 0, то её ветви направлены вниз.
Далее вспомним координату (абсциссу) вершины параболы:

То есть, это точка экстремума квадратичной функции – в ней функция меняет своё поведение с возрастания на убывание или наоборот.
Следующий важный факт (ключевой для этих задач):
Если исходная функция монотонна (непрерывно возрастает или убывает), для нее указанная точка «х» также будет точкой экстремума.
Почему? Давайте рассмотрим отдельно функции подробнее.
Квадратичная функция в показателе степени (при чём n>1):
![]()
Смотрите! Представим, что ax2+bx+c=z. Можем записать:
![]()
Получается что значение z изменяется следующим образом.
Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a z уменьшается, в точке –b/2a значение будет минимальным, далее при х от –b/2a до бесконечности z увеличивается.
Это означает, что и сама функция у=nf(x) будет имет минимальное значение в точке х=–b/2a, так как при минимуме в показателе получится минимум в результате.
Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до –b/2a z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a до бесконечности z уменьшается.
Это означает, что и сама функция у=nf(x) будет иметь максимальное значение в точке х=–b/2a, так как при максимуме в показателе получится максимум в результате.
Квадратичная функция под знаком логарифма (при чём n>1):
![]()
Представим, что ax2+bx+c=z. Можем записать:
![]()
Получается что значение z изменяется следующим образом:
Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a z уменьшается, в точке –b/2a значение будет минимальным, далее при х от–b/2a до бесконечности z увеличивается.
Это означает, что и сама функция lognz будет имет минимальное значение в точке х=–b/2a. Так как логарифмическая функция уменьшается при уменьшении аргумента (видно по графику).
Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до –b/2a z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a до бесконечности z уменьшается.
Это означает, что и сама функция lognz будет имеет максимальное значение в точке х=–b/2a. Так как логарифмическая функция увеличивается при увеличении аргумента (видно по графику).
Квадратичная функция под знаком корня:
![]()
Представим, что ax2+bx+c=z. Можем записать:
![]()
Получается что:
При a>0 значение z минимально в точке х=–b/2a, а значит и сама функция будет иметь минимальное значение. *Корень из наименьшего значения в результате даст наименьшее число.
При a<0 значение z максимально в точке х=–b/2a, а значит и сама функция будет иметь максимальное значение.
Таким образом, сформулируем ключевое правило:

ВНИМАНИЕ! Конечно, если глубже уйти в тему, то возможны варианты когда сложная функция имеет отрицательный знак, когда логарифм находится в знаменателе дроби, когда основание логарифма или основание степени находится в пределах от 0 до 1. Разумеется, важно понимать как ведёт себя данная в условии функция (возрастает или убывает). Но для решения типовых заданий экзамена указанного вывода вам будет вполне достаточно.
И конечно, не теряйте из виду область допустимых значений заданной функции:
— выражение стоящее под знаком корня, больше или равно нулю (число неотрицательное).
— выражение стоящее под знаком логарифма, есть положительное число.
— выражение стоящее в знаменателе дроби не равно нулю.
В подобных задачах на нахождение наибольшего и наименьшего значения функции, я бы посоветовал находить область определения в любом случае (даже не смотря на то, что в представленных ниже примерах это ничего важного нам не даёт и не влияет на ответ).
Рассмотрим примеры:

Найдите точку максимума функции
![]()
Под корнем квадратичная функция 13+6х–х2. Ее график — парабола, ветви направлены вниз, поскольку а=–1<0. Значит максимальное значение функция приобретает в точке:

Проверим чему равно подкоренное выражение при х=3 То есть будет ли оно числом неотрицательным:
13 + 6∙3 – 32 = 13 + 18 – 9 = 22 > 0
Почему необходимо это сделать? Дело в том, что при полученной абсциссе квадратичная функция теоретически может дать отрицательное значение, то есть график такой параболы будет лежать ниже оси ох. Это будет означать что решения (таких вариантов заданий на самом ЕГЭ не будет).
Ответ: 3
Решите самостоятельно:
Найдите точку максимума функции
![]()

Найдите наименьшее значение функции
![]()
Под корнем квадратичная функция х2 + 8х + 185.
Ее график — парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины параболы:

Так как ветви параболы направлены вверх, то в точке х = – 4 функция
х2 + 8х + 185 принимает наименьшее значение.
Функция кважратного корня монотонно возрастает, значит х = 4 точка минимума всей функции, вычислим её наименьшее значение:
![]()
Ответ: 13
Решите самостоятельно:
Найдите наименьшее значение функции
![]()

Найдите точку максимума функции у=log7(–2 – 12х – х2) + 10.
Под знаком логарифма квадратичная функция –2 – 12х – х2.
График — парабола, ветви направлены вниз, так как а = – 1 < 0
Абсцисса вершины параболы:
![]()
Проверим, принадлежит ли полученное значение х области определения (выражение под знаком логарифма должно быть число положительное):
– 2 – 12∙(–6) – (–6)2 = – 2 + 72 – 36 = 34 > 0
То есть, в точке х = – 6
функция f (х) = – 2 – 12х – х2 будет иметь максимальное значение.
Значит, и у=log7(–2–12х–х2)+10 в этой точке так же будет иметь максимальное значение.
Ответ: – 6.
Решите самостоятельно:
Найдите точку максимума функции у=log2(2 + 2х – х2) – 2

Найдите наименьшее значение функции у=log9 (х2 – 10х + 754) + 3
Под корнем квадратичная функция х2 – 10х+754.
Ее график — парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины параболы:
![]()
То есть, в точке х = 5 функция f (x) = х2 – 10х + 754 принимает наименьшее значение.
Функция log9х монотонная, значит у =log9 (х2 – 10х + 754) + 3 в точке х = 5 также принимает наименьшее значение, вычислим его:
 Ответ: 6
Ответ: 6
Решите самостоятельно:
Найдите наименьшее значение функции у=log3(х2 – 6х + 10) + 2

Найдите точку максимума функции
![]()
В показателе стоит квадратичная функция – 30 + 12х – х2.
График — парабола, ветви направлены вниз, так как а = –1 < 0.
Абсцисса вершины параболы:

То есть, в точке х = 6 функция f (х) = – 30 + 12х – х2 приобретёт максимальное значение. Значит и данная функция в этой точке будет иметь также максимальное значение.
Ответ: 6
Решите самостоятельно:
Найдите точку максимума функции:
![]()

Найдите наименьшее значение функции
![]()
В показателе стоит квадратичная функция х2 + 16х + 66.
Ее график — парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины параболы:

То есть, в точке х = – 8 функция х2 + 16х + 66 принимает наименьшее значение.
Показательная функция монотонна, поэтому её наименьшее значение будет также в точке х = – 8, вычислим его
![]()
Ответ: 36
Решите самостоятельно:
Найдите наименьшее значение функции
![]()
Разумеется, что это краткая схема решения и, конечно же, нужно понимать свойства квадратичной, показательной, логарифмической, дробно-рациональной функции, но эта схема работает.
В данной рубрике мы ещё рассмотрим задания с тригонометрическими функциями, не пропустите! Успеха вам!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.
















Почему то я так и не перешел на ты с B14.Александр,в целом задание B14 по уровню сложности самое сложное в части B?Или оно только кажется сложным?
Да, задачи с производными заставляют потрудиться. Но если таблица производных на зубок, и её свойства для исследования функций поняты, то оказывается, что сложностей как небывало.