![]()
Функции с числом е. Друзья! На сайте «Математический тандем» проходит конкурс «Лучший комментатор декабря 2012 года», так что добро пожаловать, будут призы. В данной статье мы с вами рассмотрим задачи, входящие в сотав типовых заданий экзамена по математике, связанные с исследованием функций (где присутствует число е).
Рекомендую вам ещё раз внимательно прочитать статью «Исследование функций. Это нужно знать!» и освежить в памяти изложенную информацию. Не устану повторять, что для того чтобы решать задачи на нахождение наибольшего или наименьшего значения, задачи на нахождение экстремумов, важно понимать свойства производной для исследования функций, знать таблицу производных и правила дифференцирования.
После решения каждой задачи есть разъяснения другого подхода к решению (я обещал вам «хитрости» — они здесь). Рекомендую посмотреть, выглядит график показательной функции.
Рассмотрим задачи:

Найдите наименьшее значение функции у = (х–17)ех–16
на отрезке [15;17].
Мы знаем, что для того, чтобы найти наибольшее или наименьшее значение функции на отрезке, необходимо вычислить её значение на границах заданного интервала и в точках, где производная равна нулю. Действуем по алгоритму:
1. Найдём производную заданной функции:
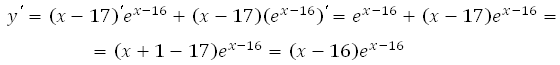
2. Найдем нули производной на заданном отрезке, то есть приравниваем производную к нулю и вычислим корни уравнения:
![]()
*Выражение ех-16 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.
3. Определяем принадлежит ли найденная точка интервалу.
Точка х = 16 принадлежит интервалу [15;17]. Значит значение функции будем вычислять в точках 15, 16 и 17:
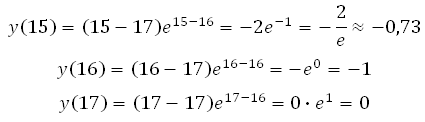
*Учтите, что число е ≈ 2,71. Это нецелое число и неконечная десятичная дробь, поэтому любое выражение с этим числом в подобных задачах на ЕГЭ не является верным ответом, но вы всё равно его проанализируйте. В данной задаче, если мы –2 разделим на число 2,71 то результат будет лежать в пределах от –1 до 0 (можно посчитать столбиком для проверки).
4. Делаем вывод.
Таким образом, наименьшее значение функции равно –1.
Ответ: –1
В этой статье я обещал вам какие-то там «хитрости», которые можно использовать при решении. Если вы поняли теорию производной и знаете, как находить максимальные и минимальные значения, то тогда читайте дальше — представленный приём будет хорошим дополнительным «инструментом» и позволит решать подобные задания мгновенно.
Итак! Мы знаем, что ответом в задачах на ЕГЭ в части В должно быть целое число, либо конечная десятичная дробь.
Посмотрите на данную функцию. Сразу можно сказать, что значение функции будет являться целым числом только при х = 16 или при х = 17, и ни при каких других значениях х. Поэтому достаточно вычислить:
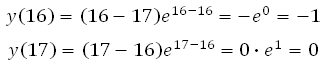
и далее записать ответ.
Ещё один путь решения (без нахождения производной). Сразу подставляем в функцию все целые значения из интервала (их всего три 15, 16 и 17), вычисляем и выбираем наименьшее значение:
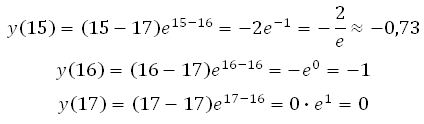
Решите самостоятельно:
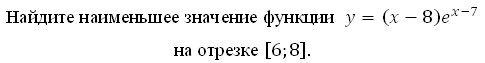

Найдите точку минимума функции у = (х + 18)ех-18
1. Найдём производную заданной функции:
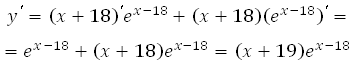
2. Найдем нули производной:
![]()
Получаем, что х = –19.
*Выражение ех-18 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.
3. Определим знаки производной функции на интервалах (подставляем любые произвольные значения в производную) и изобразим на рисунке поведение функции:
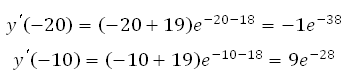
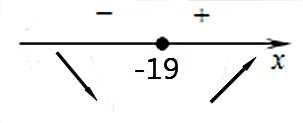
В точке х = –19 функция меняет знак с отрицательного на положительный, значит это искомая точка минимума.
Ответ: –19
Как решать быстрее данный тип задач?
Когда мы получили производную и приравняли её к нулю:
(х + 19)ех–18 = 0
Далее получили, что х=–19. Данное решение и будет являться ответом задачи.
*То есть, в при решении данного типа задач, можно обойтись без определения знаков производной на интервалах. Но будьте осторожны! В других заданиях на нахождение максимума (минимума), где получите несколько нулей производной, её знаки на интервалах нужно определять обязательно.
Решите самостоятельно:
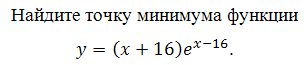

Найдите точку максимума функции у = (3х2 – 15х + 15)е7–х
Найдём производную заданной функции:
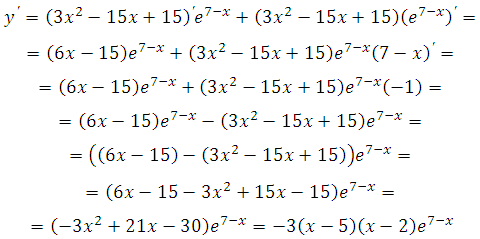
Найдем нули производной:
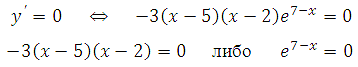
Число е7-х не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.
Решаем – 3 (х–5)(х–2) = 0. Получим х1 = 5 и х2 = 2 .
Определим знаки производной функции (подставляя любые значения из интервалов в найденную производную) и изобразим на рисунке поведение функции:
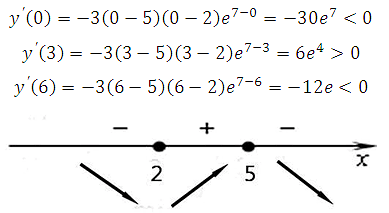
В точке х = 5 функция меняет знак с положительного на отрицательный, значит это искомая точка максимума.
Ответ: 5
Решите самостоятельно:
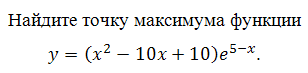

Найдите наибольшее значение функции у = (22 – х)ех–21
на отрезке [16;25].
Найдём производную заданной функции:
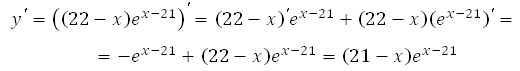
Найдем нули производной:
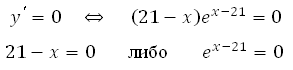
Число ех-21 не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное, значит х = 21.
Полученное значение принадлежит интервалу [16;25].
Вычислим значения данной в условии функции в точках 16, 21 и 25:
*То есть на границах интервала и в точке, где производная обращается в нуль.
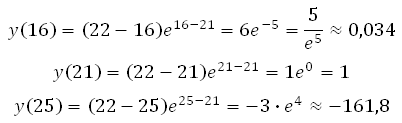
Первый результат меньше единицы (это понятно и без вычислений).
Третий результат так же меньше единицы (отрицательное число).
Значит наибольшее значение функции на заданном интервале равно 1.
*Помните, что ответы с числом е (по требованиеям ЕГЭ) не являются верными.
Ответ: 1
Если у вас всё-таки неразрешимые проблемы с нахождением производной, то подставляйте в исходную функцию все целые значения из интервала и выбирайте наибольшее полученное значение.
*Кроме того, по данной функции сразу видно, что её значение будет целым числом только при х = 21 или при х = 22.
Можете подставить только их в функцию, далее произвести вычисления и выбрать наибольшее значение.
Решите самостоятельно:

Найдите наибольшее значение функции у = (2х2 – 10х + 10)е х
на отрезке [–4; 3].
Необходимо определить значения на границах интервала, и в точках, где производная обращается в нуль.
Найдём производную заданной функции:
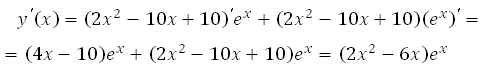
Найдем нули производной:
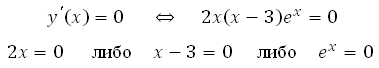
Произведение множителей равно нулю, когда какой либо из этих множителей равен нулю.
Число ех не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.
Значит решением являются корни: х1=0 и х2=3
Обе точки принадлежат интервалу [–4;3], х=3 совпадает с границей интервала.
Вычисляем значения функции в точках: – 4, 0 и 3:
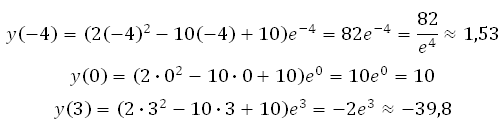
Значит наибольшее значение функции равно 10.
Ответ: 10
*Как вы уже поняли, можно в заданную функцию можно подставить все целые значения х из интервала, и таким образом найти наибольшее значение функции. Но в данном случае придётся перебрать 8 чисел (–4;–3;–2;–1;0;1;2;3).
Решите самостоятельно:
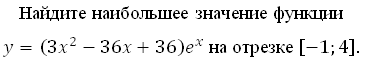

Найдите наименьшее значение функции у = (х + 44)2е–44–х
на отрезке [– 46; –43]
Найдём производную заданной функции:
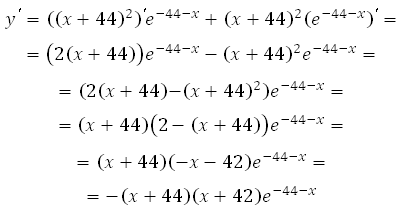
Обратите внимание, что результат мы представили сразу в виде множителей, это будет удобно при вычислении нулей производной.
Найдем нули производной:
![]()
Решением являются корни: х1= – 44 и х2= – 42.
Заданному интервалу [– 46;–43] принадлежит только точка х = – 44.
Вычисляем значения функции в точках – 46, – 44 и – 43, то есть на границах интервала и в точке, где производная равна нулю:
Наименьшее значение функции равно 0.
Ответ: 0
*Как это задание решить быстро?
Учитывая, что ответом должно быть целое число, видно что значение данной функции будет целым только при х= – 44 и х= 44.
указанному в условии интервалу принадлежит х= – 44, вычисляем:
Решите самостоятельно:
В данной рубрике продолжим рассматривать задачи, не пропустите!
На этом закончим. Всем удачи!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.








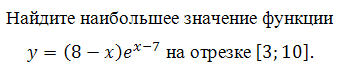
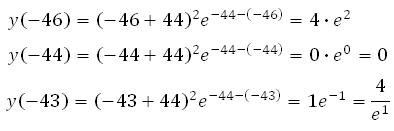








Доброго времени суток, не могли бы вы мне помочь решить данное задание:
y=(x+2)*e^1-x [-2;2]
Заранее благодарна!
Вычисляйте без производной. Просто подставляйте поочерёдно -2, -1, 0, 2, 2 и считайте. Далее увидите наибольшее или наименьшее значение.
Здравствуйте. В Вашем 3 «Найдите точку максимума функции у = (3×2 – 15х + 15)е 7–х» опечатка, или я просто не знаю откуда взялся «-» при нахождении производной. То через формулу у Вас ответ неверный.
Спасибо, что обратили внимание. Расписал подробно, и устранил описки ))