![]()
Исследование функций. В этой статье мы поговорим о задачах, в которых рассматриваются функции и в условии стоят вопросы связанные с их исследованием. Рассмотрим основные теоретические моменты, которые необходимо знать и понимать для их решения.
Это целая группа задач входящих в ЕГЭ по математике. Обычно ставится вопрос о нахождении точек максимума (минимума) или определения наибольшего (наименьшего) значения функции на заданном интервале. Рассматриваются:
Если вы поняли теорию пределов, понятие производной, свойства производной для исследования графиков функций и её геометрический смысл, то такие задачи никакого затруднения у вас не вызовут и вы решите их с лёгкостью.
Информация ниже — это теоретические моменты, понимание которых позволит осознать, как решать подобные задачи. Постараюсь изложить их именно так, чтобы даже тот, кто эту тему пропустил или изучил слабо, смог без особых затруднений решать подобные задачи.
В задачах данной группы, как уже сказано, требуется найти либо точку минимума (максимума) функции, либо наибольшее (наименьшее) значение функции на интервале.
Точки минимума, максимума. Свойства производной.
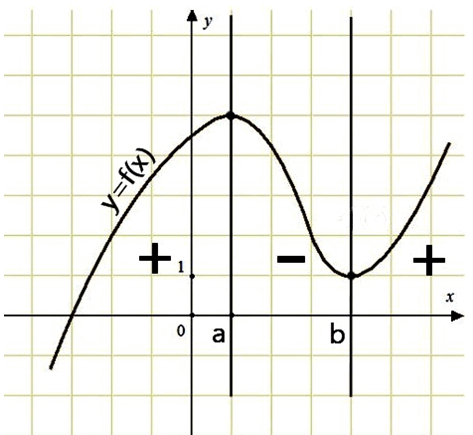
Рассмотрим график функции:
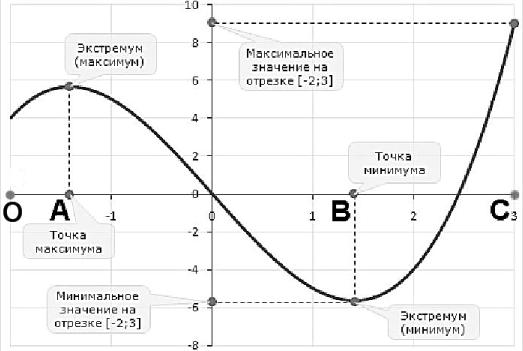
Точка А – это точка максимума, на интервале от О до А функция возрастает, на интервале от А до В убывает.
Точка В – это точка минимума, на интервале от А до В функция убывает, на интервале от В до С возрастает.
В данных точках (А и В) производная обращается в нуль (равна нулю).
Касательные в этих точках параллельны оси ox.
Добавлю, что точки, в которых функция меняет своё поведение с возрастания на убывание (и наоборот, с убывания на возрастание), называются экстремумами.
Важный момент:
1. Производная на интервалах возрастания имеет положительный знак (при подстановке значения из интервала в производную получается положительное число).
Значит, если производная в определённой точке из некоторого интервала имеет положительное значение, то график функции на этом интервале возрастает.
2. На интервалах убывания производная имеет отрицательный знак (при подстановке значения из интервала в выражение производной получается отрицательное число).
Значит, если производная в определённой точке из некоторого интервала имеет отрицательное значение, то график функции на этом интервале убывает.
Это надо чётко уяснить!!!
Таким образом, вычислив производную и приравняв её к нулю, можно найти точки, которые разбивают числовую ось на интервалы. На каждом из этих интервалов можно определить знак производной и далее сделать вывод о её возрастании или убывании.
*Отдельно следует сказать о точках, в которых производая не существует. Например, можем получить производную, знаменатель которой при определённом х обращается в нуль. Понятно, что при таком х производная не существует. Так вот, данную точку также необходимо учитывать при определени интервалов возрастания (убывания).
Функция в точках, где производная равна нулю меняет свой знак не всегда. Об этом будет отдельная статья. На самом ЕГЭ таких задач не будет.
Вышеизложенные свойства необходимы для исследования поведения функции на возрастание и убывание.
Что ещё необходимо знать для решения оговоренных задач: таблицу производных и правила дифференцирования. Без этого никак. Это базовые знания, в теме производной. Производные элементарных функций вы должны знать на отлично.
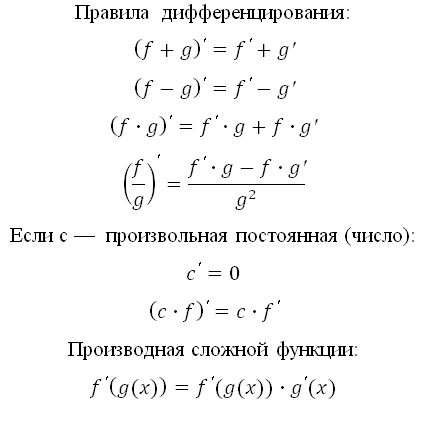
Вычисляя производную сложной функции f(g(x)), представьте, что функция g(x) это переменная и далее вычисляйте производную f’(g(x)) по табличным формулам как обычную производную от переменной. Затем полученный результат умножьте на производную функции g(x).
Посмотрите видеоурок Максима Семенихина о сложной функции:

Исследование функций
Задачи на нахождение точек максимума и минимума
Алгоритм нахождения точек максимума (минимума) функции:
1. Находим производную функции f’(x).
2. Находим нули производной (приравниванием производную к нулю f’(x)=0 и решаем полученное уравнение). Также находим точки в которых производная не существует (в частности это касается дробно-рациональных функций).
3. Отмечаем полученные значения на числовой прямой и определяем знаки производной на этих интервалах путём подстановки значений из интервалов в выражение производной.
4. Далее делаем вывод.
Вывод будет один из двух:
1. Точка максимума это точка, в которой производная меняет значение с положительного на отрицательное.
2. Точка минимума это точка, в которой производная меняет значение с отрицательного на положительное.
Задачи на нахождение наибольшего или наименьшего значения
функции на интервале.
В другом типе задач требуется найти наибольшее или наименьшее значение функции на заданном интервале.
Алгоритм нахождения наибольшего (наименьшего) значения функции:
1. Определяем, есть ли точки максимума (минимума). Для этого находим производную f’(x), затем решаем f’(x)=0 (пункты 1 и 2 из предыдущего алгоритма).
2. Определяем, принадлежат ли полученные точки заданному интервалу и записываем лежащие в его пределах.
3. Подставляем в исходную функцию (не в производную, а в данную в условии) границы данного интервала и точки (максимума-минимума), лежащие в пределах интервала (п.2).
4. Вычисляем значения функции.
5. Выбираем из полученных наибольшее (наименьше) значение, в зависимости от того, какой вопрос был поставлен в задаче и далее записываем ответ.
Вопрос: для чего в задачах на нахождение наибольшего (наименьшего) значения функции необходимо искать точки максимума (минимума)?
Ответ лучше всего это проиллюстрировать, посмотрите схематичное изображение графиков, задаваемых функций:
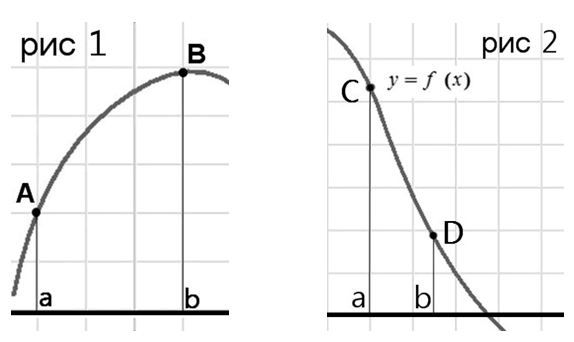
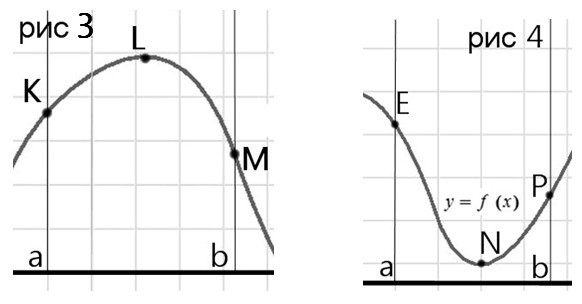
В случаях 1 и 2 достаточно подставить границы интервала, чтобы определить наибольшее или наименьшее значение функции. В случаях 3 и 4 необходимо найти нули функции (точки максимума-минимума). Если мы подставим границы интервала (не находя нули функции), то получим неверный ответ, это видно по графикам.
И всё дело в том, что мы по заданной функции не можем увидеть как выглядит график на интервале (имеет ли он максимум или минимум в пределах интервала). Потому находите нули функции обязательно!!!
Если уравнение f’(x)=0 не будет иметь решения, это значит, что точек максимума-минимума нет (рисунок 1,2), и для нахождения поставленной задачи в данную функцию подставляем только границы интервала.
Ещё один важный момент. Помните, что ответом должно быть целое число или конечная десятичная дробь. При вычислении наибольшего и наименьшего значения функции вы будете получать выражения с числом е и Пи, а также выражения с корнем. Запомните, что до конца вам их вычислять не нужно, и так понятно, что результат таких выражений ответом являться не будет. Если возникнет желание вычислить такое значение, то сделайте это (числа: е ≈ 2,71 Пи ≈ 3,14 ).
Много написал, запутал наверное? По конкретным примерам вы увидите, что всё просто.
Далее хочу открыть вам маленький секрет. Дело в том, что многие задания можно решить без знания свойств производной и даже без правил дифференцирования. Об этих нюансах я вам обязательно расскажу и покажу как это делается? не пропустите!
Но тогда зачем же я вообще изложил теорию и ещё сказал, что её нужно знать обязательно. Всё верно – знать надо. Если её поймёте, тогда никакая задача в этой теме в тупик вас не поставит.
Те «хитрости», о которых вы узнаете, помогут вам при решении конкретных (некоторых) прототипов задач. Как дополнительный инструмент эти приёмы использовать, конечно, удобно. Задачу можно решить в 2-3 раза быстрее и сэкономить время на решение части С.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.
















Спасибо большое очень хороший сайт