![]()
Пришло время в данном разделе рассмотреть степенные функции. На блоге уже представлены задания на нахождение точек максимума и минимума различных функций, а именно: функций с числом е, с логарифмами, тригонометрические, рациональные.
Алгоритм нахождения данных точек оговаривался уже неоднократно, кратко повторюсь:
1. Находим производную функции.
2. Находим нули производной (приравниваем производную к нулю и решаем уравнение).
3. Далее строим числовую ось, на ней отмечаем найденные точки и определяем знаки производной на полученных интервалах. *Это делается путём подстановки произвольных значений из интервалов в производную.
4. Далее делаем вывод.
Если вы совсем не знакомы со свойствами производной для исследования функций, то обязательно изучите статью «Исследование функций. Это нужно знать!».Также повторите таблицу производных и правила дифференцирования (имеются в этой же статье). Рассмотрим задачи:

77431. Найдите точку максимума функции у = х3–5х2+7х–5.
Найдём производную функции:
![]()
Найдем нули производной:
3х2 – 10х + 7 = 0
Решая квадратное уравнение получим:
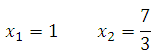
*Это точки возможного максимума (минимума) функции.
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(0)' = 3∙02 – 10∙0 + 7 = 7 > 0
у(2)' = 3∙22 – 10∙2 + 7 = – 1< 0
у(3)' = 3∙32 – 10∙3 + 7 = 4 > 0

В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 1

77432. Найдите точку минимума функции у = х3+5х2+7х–5.
Найдём производную функции:
![]()
Найдем нули производной:
3х2 + 10х + 7 = 0
Решая квадратное уравнение получим:
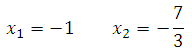
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)' = 3∙(–3)2 + 10∙(–3) + 7 = 4 > 0
у(–2)'= 3∙(–2)2 + 10∙(–2) + 7 = –1 < 0
у(0)'= 3∙02 – 10∙0 + 7 = 7 > 0
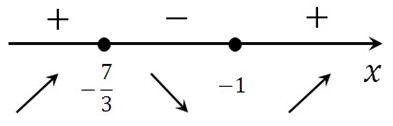
В точке х = –1 производная меняет свой знак с отрицательного на положительный, значит это есть искомая точка минимума.
Ответ: –1

77435. Найдите точку максимума функции у = 7+12х–х3
Найдём производную функции:
![]()
Найдем нули производной:
12 – 3х2 = 0
х2 = 4
Решая уравнение получим:
![]()
*Это точки возможного максимума (минимума) функции.
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)'=12 – 3∙(–3)2 = –15 < 0
у(0)'=12 – 3∙02 = 12 > 0
у(3)'=12 – 3∙32 = –15 < 0
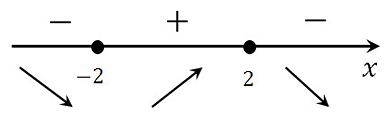
В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 2
*Для этой же функции точкой минимума является точка х = – 2.

77439. Найдите точку максимума функции у = 9х2– х3.
Найдём производную функции:
![]()
Найдем нули производной:
18х –3х2 = 0
3х(6 – х) = 0
Решая уравнение получим:
![]()
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–1)'=18 (–1) –3 (–1)2 = –21< 0
у(1)'=18∙1 –3∙12 = 15 > 0
у(7)'=18∙7 –3∙72 = –1< 0
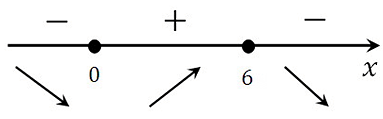
В точке х = 6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 6
*Для этой же функции точкой минимума является точка х = 0.

77443. Найдите точку максимума функции у = (х3/3)–9х–7.
Найдём производную функции:
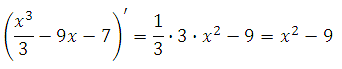
Найдем нули производной:
х2 – 9 = 0
х2 = 9
Решая уравнение получим:
![]()
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)'= (–4)2 – 9 > 0
у(0)'= 02 – 9 < 0
у(4)'= 42 – 9 > 0
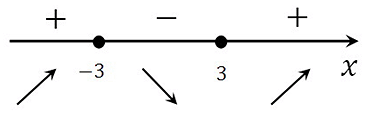
В точке х = – 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: – 3
*Для этой же функции точкой минимума является точка х = 3.

77443. Найдите точку максимума функции у = 5+9х– (х3/3).
Найдём производную функции:
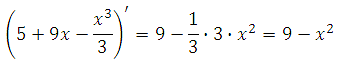
Найдем нули производной:
9 – х2 = 0
х2 = 9
Решая уравнение получим:
![]()
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)'= 9 – (–4)2 < 0
у(0)'= 9 – 02 > 0
у(4)'= 9 – 42 < 0
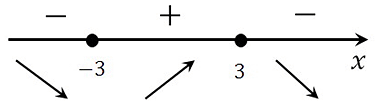
В точке х = 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 3
*Для этой же функции точкой минимума является точка х = – 3.
![]()
77419. Найдите точку максимума функции у = х3– 48х+17. Решение.
77423. Найдите точку максимума функции у = х3–3х2+2. Решение.
77427. Найдите точку максимума функции у = х3+2х2+х+3. Решение.
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
















Спасибо за прекрасную информацию в течение года. Хорошего Вам отдыха и да здравствует 2014—2015 учебный год!
Галина Михайловна, спасибо. Вам хорошего отдыха!
Огромное вам СПАСИБО! ^^ Очень полезный сайт, много хорошего материала для подготовки к экзаменам. Всё очень подробно, словно на блюдечке) Спасибо за ваш труд!
СПАСИБО большое за ваше старание ПРОЩЕ НЕ НАЙТИ НИГДЕ