![]()
Степенная функция. В данной статье мы рассмотрим вычисление максимума (минимума) указанной функции. В предыдущей статье мы с вами рассмотрели задачи на нахождение максимума (минимума) функции с числом «е». Здесь представлены примеры без числа «е». Некоторые примеры, в которых требуется найти наибольшее или наименьшее значение функции, вообще можно решить без нахождения производной.
В любом случае, советую вам ознакомится с этой статьёй, если вы ещё этого не сделали. Рассмотрим задачи:

Найдите точку максимума функции у = (х – 2)2(х – 4)+5
Для этого найдём производную, приравняем её к нулю, найдём корни полученного уравнения:
Обратите внимание, что мы сразу представили результат в виде произведения, рекомендую делать именно так. Зачем вам упрощать его до многочлена, а затем снова раскладывать его на множители? Для дальнейших действий проще сразу представить в виде произведения.
Находим нули производной:

Полученные точки разбивают числовую ость на интервалы.
Посмотрим, как ведёт себя график функции на этих интервалах. Возьмём значения из них, подставим их в производную и определим знак:

На интервале (–∞;2) функция возрастает, на интервале (2;10/3) функция убывает. Значит х = 2 это точка максимума.
Второй способ:
Перебираем значения х от – 5 до 5 подставляем в функцию и вычисляем. Затем по полученным значениям функции определяем точку максимума.
Почему берём интервал от – 5 до 5? Потому, что большинство ответов на ЕГЭ в подобных задачах лежат в этих пределах. Если будет необходимо, то берите интервал шире. Для наглядности можете построить график.
Решите предложенным способом самостоятельно, а затем посмотрите решение.
*Данный способ использовать осторожно, в будущем возможно изменение типов заданий входящих в ЕГЭ и такой подход может не сработать.
Ответ: 2

Найдите точку максимума функции у = (х – 3)2(х – 10) – 9
Это аналогичная задача.
Для этого найдём производную, приравняем её к нулю, найдём корни полученного уравнения:

Находим нули производной:

Полученные точки разбивают числовую ость на интервалы.
Посмотрим, как ведёт себя график функции на этих интервалах. Возьмём значения из интервалов, подставим их в производную и определим знак:

На интервале (–∞;3) функция возрастает, на интервале (3;23/3) функция убывает. Значит, х = 3 это точка максимума.
Вторым способом попробуйте решить сами.
Ответ: 3

Найдите наименьшее значение функции у = (х–3)2(х–6)–1 на отрезке [4;6].
Так как интервал дан (при чём он небольшой), то здесь рекомендую подставить целые значения из него (4, 5 и 6) в функцию:

Наименьшее значение функции на заданном отрезке равно – 5.
Ответ: – 5
Решите самостоятельно:


Найдите наибольшее значение функции у=(х+6)2(х–1)–6 на отрезке [– 9;–2].
Данную задачу можно решать любым из двух способов. Интервал здесь маленьким не назовёшь, но и в то же время он невелик.
Решим её подстановкой всех значений из интервала.
Подставим – 9, – 8, – 7, – 6, – 5, – 4, – 3, –2.

Наибольшее значение функции равно – 6.
Ответ: – 6
Решите самостоятельно:

Подведём итог. Как видите, задачи решаются по простому алгоритму. Важно для успешного решения знать таблицу производных, правила дифференцирования и производную сложной функции, свойства производной для исследования графиков функций.
Конечно, когда используем метод подстановки значений из интервала, то знать всё это, казалось бы, не обязательно, но такой подход помогает не всегда. Советую использовать его лишь как дополнительный инструмент.
Мы продолжим рассматривать задачи в этой рубрике, не пропустите!
Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.








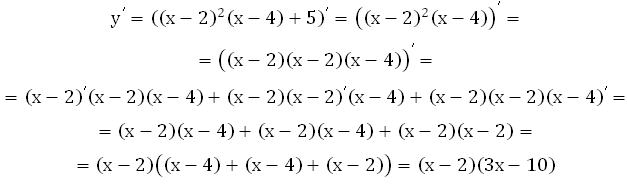








Александр,спасибо за Ваши разработки.Как репетитор,я их постоянно рекомендую ученикам.С уважением Владимир Васильевич.
Владимир Васильевич, пожалуйста. И спасибо, что рекомендуете. Вам успехов и с Наступающим!!!