Логарифмические выражения. ПРИМЕРЫ!

Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.

Приведём примеры для понимания самого смысла логарифма:

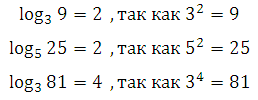
Основное логарифмическое тождество:

Свойства логарифмов, которые необходимо  всегда помнить:

*Логарифм произведения равен сумме логарифмов сомножителей.

* * *

*Логарифм частного (дроби) равен разности логарифмов сомножителей.

* * *

*Логарифм степени равен произведению показателя степени на логарифм ее основания.

* * *

*Переход к новому основанию

* * *

Ещё свойства:

* * *

Вычисление логарифмов тесно связано с использованием свойств показателей степени.

Перечислим некоторые из них:

Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный.  Например:

Следствие из данного свойства:

* * *

При возведении степени в степень основание остаётся прежним, а показатели перемножаются.

* * *

При возведении в степень произведения в эту же степень возводится каждый множитель.

Так же необходимо знать следующее свойство:

Рассмотрим примеры:

26845. Найдите значение выражения:

Использовали:

Ответ: 25

26847. Найдите значение выражения log₄ 8.

Использовали:

*Второй способ:

Ответ: 1,5

26849. Найдите значение выражения log₅ 0,2 + log_0,5 4

Использовали:

Ответ: –3

26851. Найдите значение выражения

Использовали:

*То есть, имея отношение логарифмов с одним основанием, мы также можем привести его к логарифму, в котором в основании будет стоять выражение стоящее под знаком логарифма находящегося в знаменателе, а под знаком логарифма будет выражение стоящее под знаком логарифма находящегося в числителе.

Ответ: 2

26856. Найдите значение выражения:

Использовали:

Ответ: 2

26860. Найдите значение выражения log_0,8 3 · log₃ 1,25

Использовали:

Ответ: −1

26861. Найдите значение выражения:

Ответ: 7

26883. Найдите значение выражения:

Ответ: 9

26885. Найдите значение выражения:

Ответ: 3

26892. Найдите значение выражения:

Ответ: 12

26893. Найдите значение выражения:

Ответ: – 0,5

26894. Найдите значение выражения  log₃ 8,1 + log₃ 10.

Ответ: 4

26896. Найдите значение выражения:

Ответ: 0,5

77418. Вычислите значение выражения:

Ответ: 3

77415. Найдите значение выражения log_a(ab³), если log_b a = 1/7.

Преобразуем данное выражение:

Определим значение выражения  log_a b. Нам известно, что

Используем свойство:

Следовательно  log_a b = 7. 

Таким образом:

Ответ: 22

77416. Найдите log_a(a:b³), если log_a b = 5.

Ответ: –14

77417. Найдите   log_a(a²b³), если log_a b = –2.

Ответ: –4

98467.  Най­ди­те зна­че­ние вы­ра­же­ния  log_a(a⁴b⁹), если log_b a = 1/3.

Ответ: 31

98967.  Най­ди­те   log_a(a⁷:b³), если log_a b = 10.

Ответ: –23

99467.  Най­ди­те   log_a(ab¹⁰), если log_a b = 7.

Ответ: 71

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении  простых заданий можно легко допустить ошибку.

Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!

На этом всё! Успеха Вам!

С уважением, Александр Крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.