![]()
Вычисление значений тригонометрических выражений. В этой статье мы рассмотрим несколько примеров на вычисление значений тригонометрических выражений. В одной из статей уже были представлены такие примеры, посмотрите. Что необходимо знать, понимать и уметь применять?
Это формулы приведения, формулы периодичности тригонометрических функций, чётность нечётность, знаки тригонометрических функций в четвертях тригонометрической окружности, и конечно же, как всегда, требуется внимательность при вычислениях.
Периодичность тригонометрических функций.
Подробно саму теорию о периодичности здесь разъяснять не стану, будет отдельная статья, напомню вам только сами формулы:
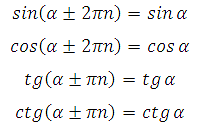
*Наименьший положительный период функции синус составляет 2Пи или 3600
*Наименьший положительный период функции косинус составляет 2Пи или 3600
*Наименьший положительный период функции тангенс составляет Пи или 1800
*Наименьший положительный период функции котангенс составляет Пи или 1800
Если вы знакомы с тригонометрической окружностью и тригонометрические функции основательно изучили, то понятие периодичности вам знакомо и смысл ясен.
Чётность и нечётность тригонометрических функций, кратко:

Рассмтотрим примеры.
*Общая рекомендация! Сначала выделяйте период и «избаляйтесь» от него, а уже затем применяйте свойство четности (нечётности) и формулы приведения.

64771. Найдите

Применим свойство периодичности синуса и формулу его приведения:

Вычислим cos α. Это можем сделать используя основное тригонометрическое тождество:
![]()
Определим знак косинуса для интервала (3П/2;2П). Это интервал от 270 до 360 градусов (четвёртая четверть). Как переводить радианы в градусы (и наоборот) можно посмотреть здесь. Значение косинуса в этой четверти положительное, поэтому:

Таким образом, 8∙cos α = 8∙0,8 = 6,4
Второй способ:

Вычисляем cos α, получаем 0,8. Таким образом:

Ответ: 6,4

64897. Найдите

Применим формулу приведения для косинуса:
![]()
Вычислим sin α. Из основного тригонометрического тождества следует, что:
![]()
Определим знак синуса для интервала (0;π/2). Это интервал от 0 до 90 градусов (первая четверть). Значение синуса в этой четверти положительное, поэтому:

Таким образом, –15∙sin α = –15∙0,96 = – 14,4
Ответ: – 14,4

65031. Найдите

Применим свойства нечётности тангенса, свойство его периодичности и формулу приведения:

Вычислим котангенс угла:

Таким образом

Ответ: – 0,8

65429. Найдите значение выражения

Используем свойство периодичности косинуса и формулу приведения синуса:

Ответ: – 2

65489. Найдите значение выражения
![]()
Используем периодичность синуса, свойство чётности косинуса и формулу приведения косинуса:

Ответ: 8

64695. Найдите значение выражения:
![]()
Решение:
![]()
Ответ: 1
![]()
26784. Найдите

26785. Найдите

26786. Найдите

26792. Найдите значение выражения

26793. Найдите значение выражения
![]()
26783. Найдите значение выражения
![]()
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.















