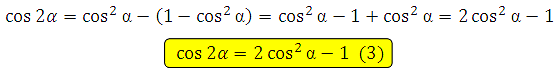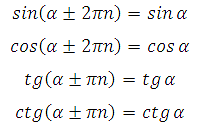![]()
Косинус двойного угла. Здесь для вас представлено ещё три примера на вычисление значений тригонометрических выражений. Процесс вычисления связан с использованием формул синуса или косинуса двойного аргумента. Вот сами формулы, их нужно выучить и всегда помнить, используются они очень часто при преобразованиях выражений:

Формулу косинуса можно представить ещё в двух вариациях.
Если мы cos2α выразим из основного тригонометрического тождества и подставим в указанную формулу, то получим:
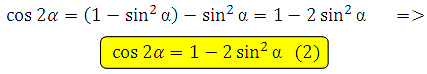
Если мы выразим sin2α из основного тригонометрического тождества и подставим в указанную формулу, то получим: