![]()
Окружность касается сторон угла, отношение радиусов окружностей. В этой статье разберём один теоретический момент, который может встретиться при решении задачи по геометрии. В любом случае, пусть данный материал будет в вашей «математической копилке», пригодится. Речь пойдёт о двух окружностях, которые лежат внутри угла, касаются его сторон и друг друга. Мы выведем формулу отношения их радиусов. Построим эскиз:
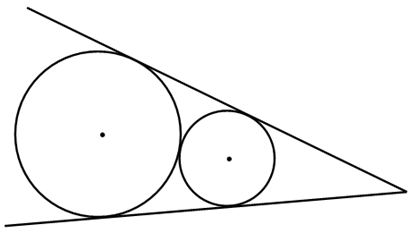
Теперь пару теорем, доказывать здесь их мы не будем, оно предельно простое.

Теорема 1: Если из одной точки, не лежащей на окружности, проведены к ней две касательные, то их отрезки равны, то есть АС=АВ.
Теорема 2: Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть АO-биссектриса.
Значит центры любых окружностей построенных таким образом будут лежать на биссектрисе угла. Теперь выполним некоторые построения и обозначим точки:

Отрезок О2F мы построили параллельно АС. Теперь обозначим:
![]()
Так как О1А биссектриса, то
![]()
Обозначим угол САВ как α (альфа), тогда
![]()
Рассмотрим прямоугольный треугольник О1О2F:

Так как FО1 = R–r, то можем записать:


Вывод: данное отношение сохранится при любом расположении окружностей, то есть независимо от их удалённости от вершины угла. Отношение радиусов зависит только от величины угла.
С уважением, Александр Крутицких.















