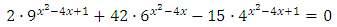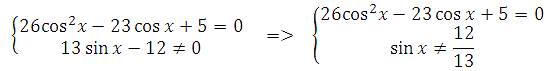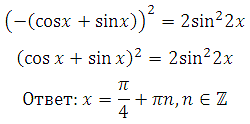Рассмотрим решение показательного уравнения. Довольно несложное уравнение, ход решения просматривается сразу. Под знаком (*) будут мои комментарии. Итак, уравнение:
Архив за №13 Урав-ия и системы

Показательное уравнение на ЕГЭ (пример)

(6 (cosx)^2-cosx-2)/(sqrt (-sinx))=0
![]()
Решите уравнение
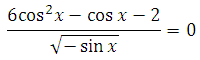
Найдём область определения. Известно, что выражение, стоящее под знаком корня должно быть больше нуля или равно ему (корень из отрицательного числа не извлекается). Кроме этого, знаменатель дроби не равен нулю (на ноль делить нельзя), значит
![]()
Мы знаем, что синус имеет отрицательное значение в третьей и четвёртой четверти тригонометрической окружности. Значит сам угол будет принадлежать в интервале от Пи до 2Пи. С учётом периода запишем: Далее

(2 (cosx)^2-2cosxcos2x-1)/(sqrt (sinx))=0
![]()
Решите уравнение
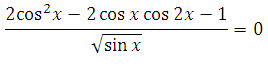
Найдём область определения для переменной. Известно, что подкоренное выражение есть число неотрицательное, кроме того, знаменатель дроби не равен нулю, значит:
![]()
Функция синуса положительна в первой и второй четверти тригонометрической окружности, это значит что:
![]()
Известно, что дробь равна нулю тогда, когда числитель равен нулю, значит: Далее

(2 (sinx)^2+2sinxcos2x-1)/(sqrt (cosx))=0
![]()
Решите уравнение
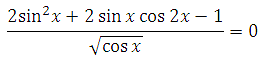
Найдём область определения уравнения. Известно, что подкоренное выражение есть число неотрицательное, кроме того знаменатель дроби должен быть не равен нулю, значит:
![]()
Функция косинуса положительна в первой и четвёртой четверти, это значит что область определения будет иметь вид: Далее

(26 (cosx)^2-23cosx+5)/(13x-12)=0
![]()
Решите уравнение
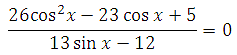
Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю. Данное уравнение равносильно системе:

Решить (2 (cosx)^2-cosx)*sqrt (-11tgx)=0
![]()
Решите уравнение
![]()
1. Найдём область допустимых значений. Известно, что подкоренное выражение есть число неотрицательное:
![]()
Кроме того известно, что для tg x
![]()
Тангенс отрицателен во второй и четвёртой четверти, поэтому учитывая выше изложенное (и периодичность тангенса), область определения уравнения имеет вид:

Решить |cosx+sinx|=(sqrt2) sin2x
![]()
Решите уравнение
![]()
1. Сразу следует отметить, что выражение
![]()
так как |cos x+sin x| имеет неотрицательное значение. Исходя из того, что корень из двух есть число положительное, получаем:
![]()
2. Используя свойство модуля, получим два уравнения, решения каждого из них будут являться решением данного уравнения: