Александр | 2014-05-18

Один отзыв

Числовые выражения, преобразование!

Числовые выражения, преобразование числовых выражений (рациональных и иррациональных). Друзья! В этой статье для вас представлено решение числовых рациональных и иррациональных выражений. Это несложные задания на ЕГЭ по математике, достаточно знать свойства степеней и корней. Ещё необходимо уметь работать с дробями (находить их сумму, разность, произведение, частное). Процесс решения такого задания занимает минуты две, не более. Не много теории:

Говоря простым (не математическим) языком рациональные выражения — это целые и дробные выражения. Ниже рассматриваются дробные выражения.

Алгебраическое выражение называется иррациональным, если в выражении, наряду с операциями сложения, вычитания, умножения и деления производится операция возведения в рациональную (не целую) степень.

Обыкновенная дробь – это отношение, вида:

Числовые выражения, преобразование числовых выражений

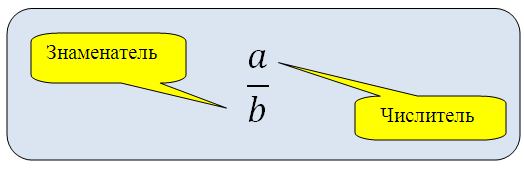
*ОТНОШЕНИЕ это есть действие — ДЕЛЕНИЕ (в данном случае «a» делим на «b»).

Также может быть записано в виде: a/b или a:b (косая черта и знак «:» означает — деление). Примеры обыкновенных дробей:

Как видно, число 4 можно записать в виде дроби 4/1. Есть дроби которые можно сократить, например, 48/8 = 6. Некоторые можно представить как конечные десятичные дроби: ½ = 0,5 ¼ = 0,25.

Если имеем целое число с дробной частью (смешанная дробь) и нам необходимо выполнить действие, то её нужно представить в виде простой дроби. Как?

Имеем число вида:

Чтобы получить дробное равное ему число, целую часть умножаем на знаменатель и прибавляем числитель, результат записываем в числитель, знаменатель остаётся прежний:

Например:

Если нужно вычислить сумму (разность) двух дробей с разными знаменателями, необходимо дроби привести к такому виду, чтобы их знаменатели были равны:

*То есть мы получили общий знаменатель путём умножения числителя и знаменателя первой дроби на знаменатель второй и умножением числителя и знаменателя второй дроби на знаменатель первой. Я намеренно не упоминаю здесь наименьшее общее кратное, так как для некоторых, закончивших школу «давно», возможна перегрузка информацией.

Весь смысл действия в том, чтобы привести дроби к общему знаменателю, так как с разными знаменателями дроби складывать нельзя. Если же дроби имеют общий знаменатель, то результатом суммы дробей будет дробь с тем же знаменателем, а числители складывают.

Если нужно вычислить произведение двух дробей, то результатом будет дробь, числитель которой равен произведению числителей этих дробей, а знаменатель равен произведению знаменателей:

Если одну дробь необходимо разделить на другую, то данное действие сводится к произведению делимого и дроби обратной делителю:

*То есть, говоря простым языком, мы «переворачиваем» ту дробь на которую делим и деление заменяем умножением.

Свойства степени и корня можно посмотреть здесь.

Рассмотрим задания:

77387. Найдите значение выражения

Ответ: 8

77389. Найдите значение выражения

Ответ: 5

77391. Найдите значение выражения

Ответ: 10

77392. Найдите значение выражения

*В данной задаче не нужно вычислять произведения и затем отношение. Глядя на числа видно, что они прекрасно сокращаются. Достаточно произвести несложные преобразования и пример вычисляется устно.

Ответ: 10

86983. Найдите значение выражения

Упрощаем, используя формулу разности квадратов

и вычисляем:

Ответ: 702

61513. Найдите значение выражения

Ответ: 24

62385. Найдите значение выражения

Ответ: 2

62647. Найдите значение выражения

Ответ: 2

68141. Найдите

Определим числитель и знаменатель:

Числитель равен знаменателю. Это означает, что отношение равно единице:

Ответ: 1

26745. Найдите значение выражения

*Если корни имеют разные степени, то преобразования с внесением выражений под один корень выполнять нельзя. Требуется привести все корни к равной степени. Используем свойство: