![]()
Показательные уравнения. Как известно — в состав ЕГЭ входят простые уравнения. Некоторые мы уже рассмотрели – это логарифмические, тригонометрические, рациональные. Здесь представлены показательные уравнения.
В недавней статье мы поработали с показательными выражениями, посмотрите, будет полезно. Сами уравнения решаются просто и быстро. Требуется лишь знать свойства показателей степени и... Об этом далее.
Перечислим свойства показателей степени:
![]()
Нулевая степень любого числа равна единице.
Далее:

Следствие из данного свойства:
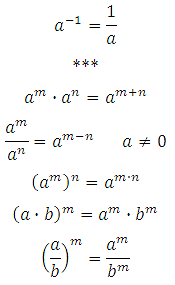
Ещё немного теории.
Показательным уравнением называется уравнение содержащее переменную в показателе, то есть это уравнение вида:
![]()
f(x) выражение, которое содержит переменную
Методы решения показательных уравнений
1. В результате преобразований уравнение можно привести к виду:
![]()
Тогда применяем свойство:
![]()
2. При получении уравнения вида a f(x) = b используется определение логарифма, получим:
![]()
3. В результате преобразований можно получить уравнение вида:
![]()
Применяется логарифмирование:
![]()
Далее применяем свойство логарифма степени:
![]()
Выражаем и находим х.
В задачах вариантов ЕГЭ достаточно будет использовать первый способ.
То есть, необходимо представить левую и правую части в виде степеней с одинаковым основанием, а далее приравниваем показатели и решаем обычное линейное уравнение.
Рассмотрим уравнения:

Найдите корень уравнения 41–2х = 64.
Необходимо сделать так, чтобы в левой и правой частях были показательные выражения с одним основанием. 64 мы можем представить как 4 в степени 3. Получим:
41–2х = 43
Основания равны, можем приравнять показатели:
1 – 2х = 3
– 2х = 2
х = – 1
Проверка:
41–2(–1) = 64
41+2 = 64
43 = 64
64 = 64
Ответ: –1


Известно, что

Значит 3х-18 = 3-2
Основания равны, можем приравнять показатели:
х – 18 = – 2
х = 16
Проверка:
316–18 = 1/9
3–2 = 1/9
1/9 = 1/9
Ответ: 16


Представим дробь 1/64 как одну четвёртую в третьей степени:

Теперь можем приравнять показатели:
2х – 19 = 3
2х = 22
х = 11
Проверка:

Ответ: 11


Представим 1/3 как 3–1, а 9 как 3 в квадрате, получим:
(3–1)8–2х = 32
3–1∙(8–2х) = 32
3–8+2х = 32
Теперь можем приравнять показатели:
– 8+2х = 2
2х = 10
х = 5
Проверка:

Ответ: 5


Решение:

Ответ: 8,75
![]()
![]()
![]()
![]()

![]()
![]()
Что хочется отметить обсобо!!!
Как бы вы не были уверены в правильности решения — ОБЯЗАТЕЛЬНО делайте проверку.
Ещё теория (чуть-чуть):
Самое простейшее показательное уравнение:

При данных условиях уравнение всегда имеет решение, при том единственное.
Действительно, при а > 1 показательная функция монотонно возрастает, а при 0 < а < 1 — монотонно убывает. В любом случае, она принимает каждое своё значение ровно один раз (видно по графику):

А вот если b < 0, то уравнение не имеет решений, ведь показательная функция может принимать только положительные значения.
Действительно, в какую бы степень мы не возвели положительное число a, мы никак не можем получить число отрицательное.
Любое показательное уравнение после соответствующих преобразований сводится к решению одного или нескольких простейших.В данной рубрике мы ещё рассмотрим решение некоторых уравнений, не пропустите! На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.















