Логарифмические уравнения!

   Логарифмические уравнения. Продолжаем рассматривать задачи из части В ЕГЭ по математике. Мы с вами уже рассмотрели решения некоторых уравнений в статьях «Тригонометрические уравнения», «Решение рациональных уравнений». В этой статье рассмотрим логарифмические уравнения. Сразу скажу, что никаких сложных преобразований при решении таких уравнений на ЕГЭ не будет. Они просты.

Достаточно знать и понимать основное логарифмическое тождество, знать свойства логарифма. Обратите внимание на то, то после решения ОБЯЗАТЕЛЬНО нужно сделать проверку — подставить полученное значение  в исходное уравнение и вычислить, в итоге должно получиться верное равенство.

Определение: 

Логарифмом числа a  по основанию b называется показатель степени, в который нужно возвести b, чтобы получить a.

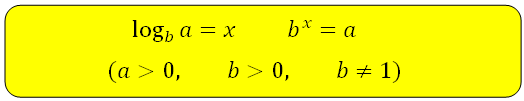
Основное логарифмическое тождество:

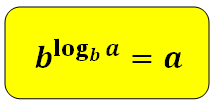
Например:

 log₃9 = 2, так как  3² = 9

Свойства логарифмов:

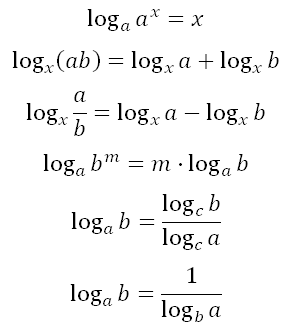
Частные случаи логарифмов:

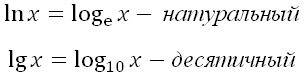
Решим задачи. В первом примере мы сделаем проверку. В последующих проверку сделайте самостоятельно.

Найдите корень уравнения:  log₃(4–x) = 4

Используем основное логарифмическое тождество.

Так как  log_ba = x   b^x = a,  то

3⁴ = 4 – x

x = 4 – 81

x =  – 77

Проверка:

log₃(4–(–77)) = 4

log₃81 = 4

3⁴ = 81  Верно.

Ответ: – 77

Решите самостоятельно:

Найдите корень уравнения:  log₂ (4 – x) = 7

Посмотреть решение 

Найдите корень уравнения log₅ (4 + x) = 2

Используем основное логарифмическое тождество.

Так как   log_ab = x       b^x = a,   то

5² = 4 + x

x =5² – 4

x = 21

Проверка:

log₅(4 + 21) = 2

log₅25 = 2

5² = 25 Верно.

Ответ: 21

Найдите корень уравнения  log₃(14 – x) = log₃5.

Имеет место следующее свойство, смысл его таков: если в левой и правой частях уравнения имеем логарифмы с одинаковым основанием, то можем приравнять выражения, стоящие под знаками логарифмов.

 Если    log_ca = log_cb,   то  a = b

14 – x = 5

x = 9

Сделайте проверку.

Ответ: 9

Решите самостоятельно:

Найдите корень уравнения  log₅(5 – x) = log₅3.

Посмотреть решение 

Найдите корень уравнения: log₄(x + 3) = log₄(4x – 15).

Если   log_ca = log_cb,   то  a = b

x + 3 = 4x – 15

3x = 18

x = 6

Сделайте проверку.

Ответ: 6

Найдите корень уравнения   log_1/8(13 – x) = – 2.

(1/8)^–2 = 13 – x

8² = 13 – x

x = 13 – 64

x = – 51

Сделайте проверку.

Небольшое дополнение – здесь используется свойство

степени (отрицательная степень дроби).

Ответ: – 51

Решите самостоятельно: 

Найдите корень уравнения:  log_1/7(7 – x) = – 2

Посмотреть решение 

Найдите корень уравнения  log₂ (4 – x) = 2 log₂ 5.

Преобразуем правую часть. воспользуемся свойством:

log_ab^m = m∙log_ab

log₂(4 – x) = log₂5²

Если    log_ca = log_cb,   то  a = b

4 – x = 5²

4 – x = 25

x = – 21

Сделайте проверку.

Ответ: – 21

Решите самостоятельно: 

Найдите корень уравнения:  log₅(5 – x) = 2 log₅ 3

Посмотреть решение 

Решите уравнение   log₅(x² + 4x) = log₅(x² + 11)

Если    log_ca = log_cb,   то  a = b

x² + 4x = x² + 11

4x = 11

x = 2,75

Сделайте проверку.

Ответ: 2,75

Решите самостоятельно: 

Найдите корень уравнения  log₅(x² + x) = log₅(x² + 10).

Посмотреть решение 

Решите уравнение   log₂(2 – x) = log₂(2 – 3x) +1.

Необходимо с правой стороны уравнения получить выражение вида:

log₂ (......)

Представляем 1 как логарифм с основанием 2:

1 = log₂ 2

Далее применяем свойство:

log_с(ab) = log_сa + log_сb

log₂(2 – x) = log₂(2 – 3x) + log₂2

Получаем:

log₂(2 – x) = log₂ 2 (2 – 3x)

Если    log_ca = log_cb,   то  a = b, значит

2 – x = 4 – 6x

5x = 2

x = 0,4

Сделайте проверку.

Ответ: 0,4

Решите самостоятельно: 

Найдите корень уравнения  log₅(7 – x) = log₅(3 – x) +1

Посмотреть решение 

Решите уравнение log_х–125 = 2.  Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Воспользуемся основным логарифмическим тождеством:

(x – 1)²= 25

Далее необходимо решить квадратное уравнение. Кстати, квадратное уравнение, как вы поняли, это очень важная «буковка» в математической азбуке. К нему сводятся очень многие решения совершенно различных задач. Помнить формулы дискриминанта и корней нужно обязательно, и уметь решать такое уравнение вы должны очень быстро, периодически практикуйтесь.

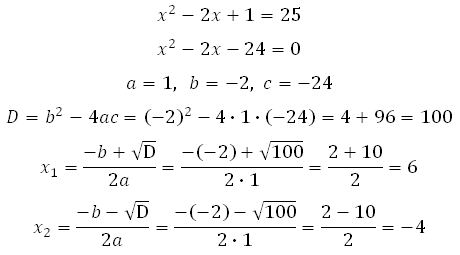
Конечно же, опытный глаз сразу увидит, что в нашем примере выражение, стоящее под знаком квадрата равно 5 или – 5, так как только эти два числа  при возведении в квадрат дают 25, устно можно посчитать:

корни равны 6  и  – 4.

Корень  "–4" не является решением, так как основание логарифма должно быть больше нуля, а при  "– 4" оно равно «–5». Решением является корень 6. Сделайте проверку.

Ответ: 6.

Решите самостоятельно: 

Решите уравнение log_x–5 49 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Посмотреть решение

Как вы убедились, никаких сложных преобразований с логарифмическими уравнениями нет. Достаточно знать  свойства логарифма и уметь применять их. В задачах ЕГЭ, связанных с преобразованием логарифмических выражений, выполняются более серьёзные преобразования и требуются более глубокие навыки в решении. Такие примеры мы рассмотрим, не пропустите! Успехов вам!!!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.