ВЫБЕРИ репетитора! Промокод на скидку 25283
НОУТБУК за 16000 рублей!

Метка: ЕГЭ-№8

|
2 комментария

В скольких точках производная функции положительна

В этой статье мы рассмотрим несколько задач связанных со свойствами производной функции. Задачи этого типа чрезвычайно просты. Повторять теорию я здесь не буду, она уже подробно изложена на блоге. Рекомендую изучить следующие статьи «Исследование функций. Это нужно знать!» и «Применение производной к исследованию графиков функций», после чего вопросов у вас не останется.

Что хотелось бы отметить особо! При прочтении условия сразу отмечайте какой график дан: график функции или график производной функции. Это важно! Часто именно из-за такой невнимательности выпускники допускают ошибки. Например, график производной принимают за график самой функции и соответственно получают неверный ответ. Рекомендую также изучить статью «Дан график производной функции. Задачи!», в которой схожие задания уже были разобраны. Рассмотрим задачи:

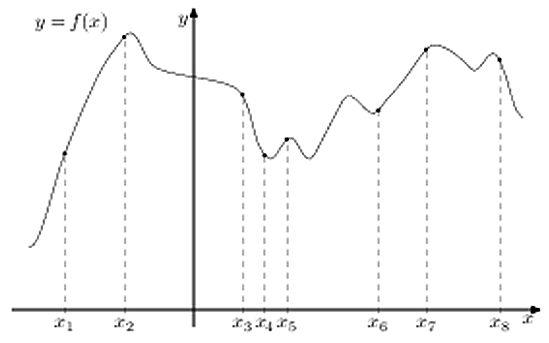
317539. На рисунке изображён график функции у = f(x)  и восемь точек на оси абсцисс: x1, x2,  x3, …,  x8. В скольких из этих точек производная функции  f(x)  положительна?

Далее

Категория: Производная Графики Функции MAX MIN | ЕГЭ-№8
|
7 комментариев

В какой точке значение производной наибольшее?

Дорогие друзья! В  группу заданий связанных с производной входят  задачи —  в условии дан график функции, несколько точек на этом графике и стоит вопрос:

В какой точке значение производной наибольшее (наименьшее)?

Данные задачи очень просты, не требуется никаких вычислений, решаются устно. Главное что необходимо – это понимать геометрический смысл производной, свойства производной для исследования функций. По представленным ссылкам вы можете повторить (изучить) материал на сайте, также краткая информация есть в справочнике.

Кратко повторим:

Производная в точке равна угловому коэффициенту касательной проходящей через эту точку графика.

Угловой коэффициент касательной в свою очередь равен тангенсу угла наклона этой касательной.

*Имеется ввиду угол между касательной и осью абсцисс.

Далее

Категория: Функции MAX MIN | ЕГЭ-№8Производная
|
7 комментариев

На рисунке изображён график производной функции

  Здравствуйте! Ударим по приближающемуся ЕГЭ качественной систематической подготовкой, и упорством в измельчении гранита науки!!! В конце  поста имеется конкурсная задача, будьте первым! В одной из статей данной рубрики мы с вами рассматривали задачи, в которых был дан график функции, и ставились различные вопросы, касающиеся экстремумов, промежутков возрастания (убывания) и прочие.

В этой статье рассмотрим задачи входящие в ЕГЭ по математике, в которых дан график производной функции, и ставятся следующие вопросы: Далее

Категория: Производная Графики Функции MAX MIN | ЕГЭ-№8
|
6 комментариев

Парабола и касательная. Находим a,b,c!

Здравствуйте! Продолжаем рассматривать задачи входящие в состав экзамена по математике. Задания, которые мы рассмотрим ниже, по-большому счёту, никаких глубоких знаний теории не требуют. Для их решения необходимо понимание геометрического смысла производной, умение решать квадратное уравнение и немного логики.

Суть заданий следующая: дана парабола вида у = ах2+bх+c и касательная к этой параболе у=kх+b. Один из коэффициентов  (a, b или c) неизвестен и его необходимо найти.

Как решать такие задачи? Что необходимо вспомнить?

1. Если даны уравнения двух функций, то точка (точки) пересечения их графиков находится путём решения системы этих уравнений. Пара (х;у) являющаяся решением системы есть точка пересечения графиков (или пары, если точек пересечения больше).

2. Если к графику функции проведена касательная, то производная этой функции в точке касания равна угловому коэффициенту этой касательной (см. ссылку выше).

Рассмотрим задачи (показаны два способа решения): Далее

Категория: Производная Графики | ЕГЭ-№8Производная
|
7 комментариев

Прямая является касательной к графику функции

   Продолжаем рассматривать задачи входящие в состав экзамена по математике. В курсе алгебры есть группа задач, где задаётся уравнение функции и уравнение прямой — касательной к графику данной функции или прямой параллельной этой касательной.

Задачи несложные, но они требуют чёткого понимания геометрического смысла производной. Это теоретическая основа для решения подобных задач (и подобных им), и без этой основы никак нельзя. Рекомендую ознакомиться со статьями «Геометричесий смысл произвоной. Часть 1» и «Геометрический смысл производной. Часть 2».

Рассмотрим две задачи:

Прямая у = 4х + 8 параллельна касательной к графику функции

у = х2 – 5х + 7 

Найдите абсциссу точки касания.

Далее

Категория: Производная Графики | ЕГЭ-№8Производная
|
2 комментария

Физический смысл производной. Задачи!

    Физический смысл производной. В состав ЕГЭ по математике входит группа задач для решения которых необходимо знание и понимание физического смысла производной. В частности, есть задачи, где дан закон движения определённой точки (объекта), выраженный уравнением и требуется найти его скорость в определённый момент времени движения, либо время, через которое объект приобретёт определённую заданную скорость. Задачи очень простые, решаются  они  в одно действие. Итак:

Пусть задан закон движения материальной точки x (t) вдоль координатной оси, где x координата движущейся точки, t – время.

Скорость в определённый момент времени – это производная координаты по времени. В этом и состоит механический смысл производной.

Далее

Категория: Производная Графики | ЕГЭ-№8Производная
|
Отзывов нет

На рисунке изображён график некоторой функции

    Здравствуйте, друзья! В данной статье рассмотрим с вами задания на первообразную. Эти задания входят в ЕГЭ по математике. Несмотря на то, что сами разделы — дифференцирование и интегрирование довольно ёмки в курсе алгебры и требуют ответственного подхода к пониманию, но сами задачи, которые входят в открытый банк заданий по математике и будут на ЕГЭ чрезвычайно просты и решаются в одно-два действия.

Важно понять именно суть первообразной и в частности геометрический смысл интеграла. Рассмотрим кратко теоретические основы.

Геометрический смысл интеграла

Кратко об интеграле можно сказать так: интеграл – это  площадь.

Определение: Пусть на координатной плоскости дан график положительной функции f, заданной на отрезке [a;b]. Подграфиком (или криволинейной трапецией) называется фигура, ограниченная графиком функции f, прямыми х = а и х= b и осью абсцисс. 

Определение: Пусть дана положительная функция f, определённая на конечном отрезке [a;b]. Интегралом от функции f на отрезке [a;b] называется площадь её подграфика.

Обозначение интеграла. Традиционно интеграл от функции у = f (x) обозначается так: Далее

Категория: Производная Графики | ЕГЭ-№8