Здравствуйте, друзья! В данной статье рассмотрим с вами задания на первообразную. Эти задания входят в ЕГЭ по математике. Несмотря на то, что сами разделы — дифференцирование и интегрирование довольно ёмки в курсе алгебры и требуют ответственного подхода к пониманию, но сами задачи, которые входят в открытый банк заданий по математике и будут на ЕГЭ чрезвычайно просты и решаются в одно-два действия.
Важно понять именно суть первообразной и в частности геометрический смысл интеграла. Рассмотрим кратко теоретические основы.
Геометрический смысл интеграла
Кратко об интеграле можно сказать так: интеграл – это площадь.
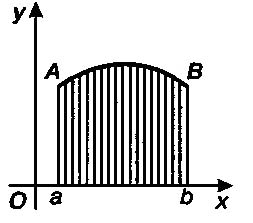
Определение: Пусть на координатной плоскости дан график положительной функции f, заданной на отрезке [a;b]. Подграфиком (или криволинейной трапецией) называется фигура, ограниченная графиком функции f, прямыми х = а и х= b и осью абсцисс.
Определение: Пусть дана положительная функция f, определённая на конечном отрезке [a;b]. Интегралом от функции f на отрезке [a;b] называется площадь её подграфика.
 Обозначение интеграла. Традиционно интеграл от функции у = f (x) обозначается так:
Обозначение интеграла. Традиционно интеграл от функции у = f (x) обозначается так: 
Первообразная
Интегрирование является операцией обратной дифференцированию. Вычисление интеграла сводится к нахождению функции, производная которой равна заданной функции.
Определение: функцию F (x) называют первообразной для функции f (х) на заданном промежутке, если для всех х из этого промежутка выполняется равенство
F′(x) = f (x)
Можно прочесть двумя способами:
f производная функции F
или
F первообразная для функции f
Для обозначения первообразной используют знак неопределённого интеграла, то есть интеграла без указания пределов интегрирования:

Теорема (Ньютона–Лейбница): Пусть f (х) данная функция, F её произвольная первообразная. Тогда

То есть, интеграл функции f (x) на интервале [a;b] равен разности первообразных в точках b и a.
Это краткое изложение теоретических основ. Есть ещё свойства интеграла, понятие интегральных сумм и прочее. Полное понимание темы требует глубокого проникновения в неё. Но то, что потребуется при решении простых задач представлено выше.
Рекомендую повторить свойства производной для исследования графиков функции, их понимание также необходимо при решении некоторых задач на первообразную.
Рассмотрим задачи:

На рисунке изображён график функции y = F (x) — одной из первообразных некоторой функции f (x), определённой на интервале (–3;5). Пользуясь рисунком, определите количество решений уравнения f (x) = 0 на отрезке [–2;4].
Как уже сказано F′(x) = f (x). Какой можем сделать вывод?
Он простой. Нам нужно определить сколько имеется точек на данном графике, в которых F′(x) = 0. Мы знаем, что производная равна нулю в тех точках, где касательная к графику функции параллельна оси ох. Покажем эти точки на интервале [–2;4]:

Это точки экстремума данной функции F (x). Их десять.
Ответ: 10

323078. На рисунке изображён график некоторой функции y = f (x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F (8) – F (2), где F (x) — одна из первообразных функции f (x).

Ещё раз запишем теорему Ньютона–Лейбница: Пусть f данная функция, F её произвольная первообразная. Тогда
 То есть, нам необходимо найти:
То есть, нам необходимо найти:
А это, как уже сказано, есть площадь подграфика функции.
Таким образом, задача сводится к нахождению площади трапеции (интервал от 2 до 8):

Её не сложно вычислить по клеткам. Получаем 7. Знак положительный, так как фигура расположена выше оси ох (или в положительной полуплоскости оси оу).
Ещё в данном случае можно было сказать так: разность значений первообразных в точках есть площадь фигуры.
Ответ: 7

323079. На рисунке изображён график некоторой функции y = f (x). Функция F (x) = x3+30x2+302x–1,875 — одна из первообразных функции y= f (x). Найдите площадь закрашенной фигуры.

Как уже сказано о геометрическом смысле интеграла это есть площадь фигуры ограниченной графиком функции f (x), прямыми х = а и х = b и осью ox.
Теорема (Ньютона–Лейбница):

Таким образом, задача сводится к вычислению определённого интеграла данной функции на интервале от –11 до –9, или другими словами нам необходимо найти разность значений первообразных вычисленных в указанных точках:

Ответ: 6

323080. На рисунке изображён график некоторой функции y = f (x).
Функция F (x) = –x3–27x2–240x– 8 — одна из первообразных функции f (x). Найдите площадь закрашенной фигуры.

Задача сводится к вычислению определённого интеграла данной функции на интервале от –10 до –8:

Ответ: 4
Ещё одно решение данной задачи, с сайта РЕШУ ЕГЭ.
Найдем формулу, задающую функцию f (x) график которой изображён на рисунке.
![]()
Следовательно, график функции f (x) получен сдвигом графика функции у = 3 – 3х2 на 9 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции у=3–3х2 и отрезком [–1;1] оси абсцисс. Имеем:

Конечно, этот способ требует: основательно знания правил дифференцирования, свойств интеграла, таблицы производных, таблицы интегралов, умения выделять неполный квадрат; владения приёмами преобразований графиков и, конечно, должна быть хорошая практика.
Ответ: 4
Таблицы производных и интегралов вы можете посмотреть.
Производные и правила дифференцирования ещё есть в этой статье. Знать их нужно обязательно, не только для решения таких заданий.
В этой рубрике продолжим рассматривать задачи, не пропустите!
Также можете посмотреть справочную информацию на сайте здесь и здесь.
Посмотрите небольшой ролик, это отрывок из фильма «Невидимая сторона». Можно сказать, что это фильм об учёбе, о милосердии, о важности якобы «случайных» встреч в нашей жизни... Но этих слов будет недостаточно, рекомендую посмотреть сам фильм, очень рекомендую.
Успехов вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.


















