Парабола и касательная. Находим a,b,c!

Здравствуйте! Продолжаем рассматривать задачи входящие в состав экзамена по математике. Задания, которые мы рассмотрим ниже, по-большому счёту, никаких глубоких знаний теории не требуют. Для их решения необходимо понимание геометрического смысла производной, умение решать квадратное уравнение и немного логики.

Суть заданий следующая: дана парабола вида у = ах²+bх+c и касательная к этой параболе у=kх+b. Один из коэффициентов  (a, b или c) неизвестен и его необходимо найти.

Как решать такие задачи? Что необходимо вспомнить?

1. Если даны уравнения двух функций, то точка (точки) пересечения их графиков находится путём решения системы этих уравнений. Пара (х;у) являющаяся решением системы есть точка пересечения графиков (или пары, если точек пересечения больше).

2. Если к графику функции проведена касательная, то производная этой функции в точке касания равна угловому коэффициенту этой касательной (см. ссылку выше).

Рассмотрим задачи (показаны два способа решения):

Прямая у=х+7 является касательной к графику функции ах²–15х+15. Найдите a.

Прямая и график  данной функции имеют одну общую точку, это значит, что данные уравнения можно внести для решения в одну систему, но этих уравнений будет недостаточно для решения (кроме неизвестных х и у имеется ещё параметр а).

Известно, что производная функции  в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть f′(x_o) = k.  Это третье уравнение, запишем систему:

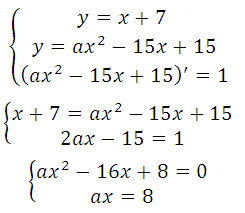
Подставим   из второго уравнения в первое:

Найдём а, подставим х = 1   в    ах² – 15х + 15 = х + 7   или   в   2ах – 15 = 1

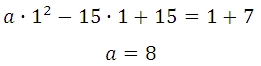
Второй способ:

По смыслу задачи параметр  a ≠ 0,  график заданной функции — парабола. Прямая с параболой имеет  единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение ах² – 15х + 15 = х + 7   имело единственно решение:

Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:

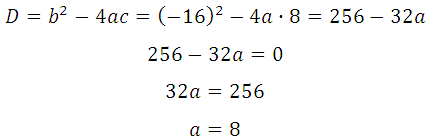
Ответ: 8

Решите самостоятельно:

Прямая у=3х+1 является касательной к графику функции ах²+2х+3. Найдите a.

Посмотреть решение

Прямая у=5х–8 является касательной к графику функции 6х² + bх + 16

Найдите b, учитывая, что абсцисса точки касания больше 0.

Прямая и парабола пересекаются в одной точке, поэтому оба уравнения можно внести в систему, но она не решаема, так как имеем три неизвестных:

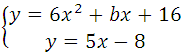
Известно, что производная функции в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть  f′(x_o) = k. Это третье уравнение, запишем систему:

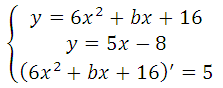
Кратко можно сказать так:

Условия касания графика функции f (x) = k и прямой у = kх + b задаётся системой требований:

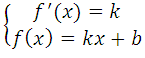
Решаем систему:

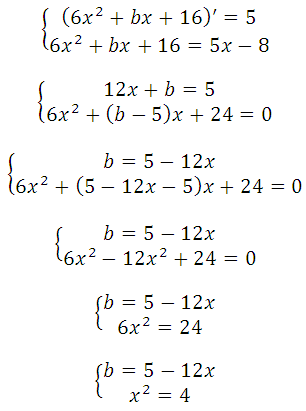
По условию, абсцисса точки касания положительна, значит х = 2.

Таким образом,

Второй способ:

График заданной функции — парабола. Прямая с параболой имеет  единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение

имело единственно решение. Преобразуем:

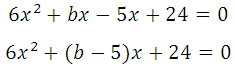
Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:

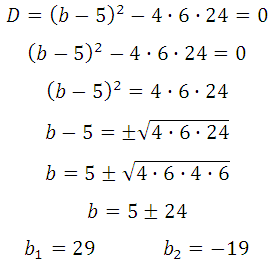
Теперь определим, при каком значении b абсцисса точки касания будет больше нуля. Можно подставить поочерёдно полученные значения в систему:

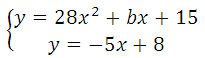
Далее решить её и сдать вывод. Верным решением будет то значение b, при котором получим положительную абсциссу.

Но мы сразу подставим их (поочерёдно)  в  28х² + (b – 5) + 24 = 0.

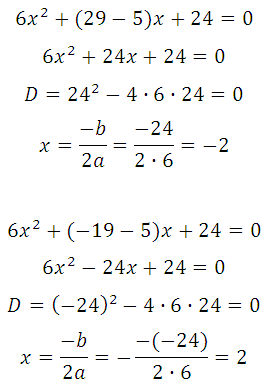
Таким образом, b = – 19 (при этом значении абсцисса точки касания положительна).

Ответ: – 19

Решить самостоятельно:

Прямая у = –5х+8 является касательной к графику функции 28х² + bх + 15.

Найдите b, учитывая, что абсцисса точки касания больше 0.

Посмотреть решение

Прямая у=–6х–2 является касательной к графику ф-ии 18х²+6х+с. Найдите c.

Условия касания графика функции у = f (x) и прямой у = kx + b задаётся системой требований:

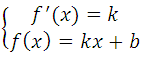
Решаем систему:

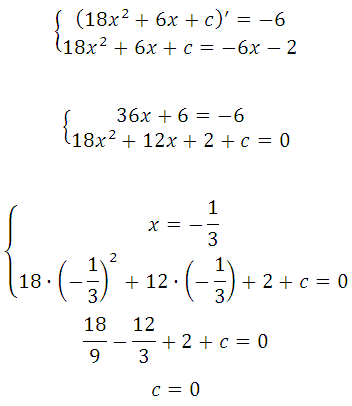
Второй способ:

График заданной функции — парабола. Прямая с параболой имеет  единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнениеимело единственное решение, преобразуем:Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю, значит: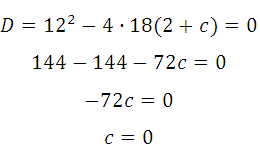Ответ: 0

Решить самостоятельно:

Прямая у=3х+4 является касательной к графику функции 3х²–3х+с. Найдите c.

Посмотреть решение

Как видим, понимание способа нахождения точки пересечения  графиков функций, заключающееся в решении системы, пригодилось при решении указанных задач (на ЕГЭ могут быть и другие). Но какие бы они не были, если чётко уясните геометрический смысл производной, проблем с подобными у вас не будет. 

В данной рубрике продолжим рассматривать задачи, не пропустите!

Имеется круглая мишень радиуса R. На ней отмечены две окружности, радиусы которых равны 1/3 и 2/3 от радиуса мишени. Какова вероятность того, что кинутый в мишень дротик попадёт в закрашенную часть мишени? Результат округлите до тысячных.

*Учесть, что дротик мимо мишени попасть не может.

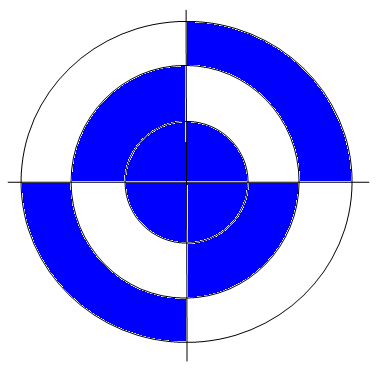
Тот учащийся, который первый напишет верный ответ, получит поощрительный приз в размере 150 рублей 😉

Надеюсь материал был вам полезен. Успехов Вам!

С уважением, Александр

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.