Задачи на работу про рабочих и детали

     Задачи на работу решаются просто. В этой статье мы с вами рассмотрим типовые задания условия которых связаны с рабочими изготавливающими детали. Алгоритм решения задач идентичен алгоритму решения задач на движение. Перед дальнейшим изучением материала обязательно посмотрите статью, где мы решали задания на движение. Итак, формула:

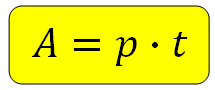
Здесь A — работа, t — время, а величина p, которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, Вася красит забор. Количество метров, которые он красит за час — это и есть его производительность. То есть это скорость работы.

Правила решения задач на работу:

1. А = р∙t, из этой формулы легко найти t или p.

2. Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти  — работа принимается за единицу. Построен дом (один), покрашен забор (один), наполнен резервуар. А вот если речь идет о количестве кирпичей, количестве деталей, литрах воды  —  работа как раз и равна этому количеству.

3. Если трудятся двое рабочих (два экскаватора, два мастера, Даша и Маша...) или трое (не важно)  — их производительности суммируются. Очень логичное правило.

4. В качестве переменной «х» удобно взять (в абсолютном большинстве задач) именно производительность. Так же, как в задах на движение мы за «х» принимаем скорость.

Вы убедитесь, что задачи на работу  и движение очень схожи.

Рассмотрим задачи:

Заказ на 240 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?

Как и в задачах на движение, заполним таблицу.

В колонке «работа» и для первого, и для второго рабочего запишем: 240. В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем её  за х. Тогда производительность первого рабочего равна  х + 1 (он делает на одну деталь в час больше).

Поскольку t = A/p,  время работы первого рабочего равно  t₂ = 240/(х + 1),  время работы второго равно t₂ = 240/х.

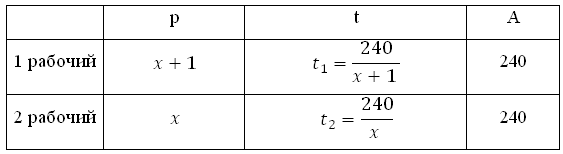
Первый рабочий выполнил заказ на час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй, то есть t₁   на 1 меньше, чем t₂,  значит

Мы уже решали такие уравнения. Оно легко сводится к квадратному:

Очевидно, производительность рабочего не может быть отрицательной величиной.  Значит, отрицательный корень не подходит.

Ответ: 15

Решить самостоятельно:

Посмотреть решение

26593. Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше?

В колонке «работа» и для первого, и для второго рабочего запишем 156.

В задаче спрашивается, сколько деталей в час делает первый рабочий, то есть какова его производительность. Примем её  за х (деталей в час). Тогда производительность второго рабочего будет равна х–1 (он делает на одну деталь в час меньше).

Поскольку t=A/p, то время работы первого рабочего будет равно:Время работы второго равно:Занесём данные в таблицу:

Первый рабочий выполнил заказ на час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй. ЗначитМожем записать:Уравнение сводится к квадратному:

Очевидно, что производительность рабочего не может быть отрицательной величиной.  Таким образом производительность первого рабочего равна 13 деталей в час.

Ответ: 13

На изготовление 40 деталей первый рабочий затрачивает на 6 часов  меньше, чем второй рабочий на изготовление 70 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий?

Данная задача практически не отличается от предыдущей, разница лишь в объёме работы. Примем производительность второго рабочего за х.

Тогда производительность первого рабочего равна х + 3 (он делает  в час  на три детали больше).  Заполним графу «время» в таблице:

Сравнение будем проводить по времени. Сказано, что первый затрачивает на 6 часов меньше, чем второй. Значит

Таким образом, второй рабочий в час делает 7 деталей.

Ответ: 7

26594. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?

Для удобства занесём данные в таблицу.

В колонке «работа» для первого запишем 475, для второго рабочего запишем 550. В задаче спрашивается, сколько деталей в час делает первый рабочий, то есть какова его производительность. Примем её  за х (деталей в час).

Тогда производительность второго рабочего будет равна х–3 (он делает на три детали в час меньше).

Поскольку t=A/p, то время работы первого рабочего будет равно

Время работы второго равноЗанесём данные в таблицу:

Сказано, что первый рабочий тратит на свой заказ на 6 часов меньше. Можем записать:

Уравнение сводится к квадратному:

Очевидно, что производительность рабочего не может быть величиной.   Первый рабочий делает 25 деталей в час.

Ответ: 25

Решить самостоятельно:

Посмотреть решение

На этом всё. В будущем мы рассмотрим задачи на работу, которые несколько отличаются от представленных выше.  Но вы увидите, что и в них нет ничего особо сложного, не пропустите!  Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.