![]()
Здравствуйте, Дорогие друзья! В данной статье мы рассмотрим задачу, которая появилась в открытом банке заданий относительно недавно. Она на прямолинейное движение. Примечательно, что при решении можно «застрять» минут на 10-20, а можно решить всего за минуту. Ниже рассмотрены оба способа — долгий и быстрый.
На блоге уже имеется ряд статей с задачами на движение (в том числе и на прямолинейное), посмотрите обязательно. Там есть необходимая теория и решения других типовых задач.
В ходе решения вы можете вносить данные в таблицу или просто записывать свои логические выводы в свободной форме — самое главное чтобы понимали суть рассуждений. Рассмотрим задачи:
323849. Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 4,4 км от места отправления. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
Процесс движения описанный в условии выглядит следующим образом:
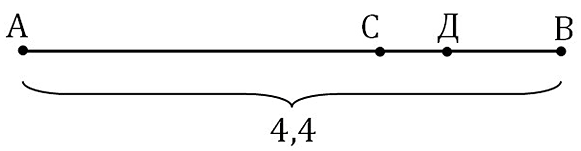
Двое выходят из точки «А» с разными скоростями. Когда второй доходит до точки «В», то первый (шедший с меньшей скоростью) находится в некой точке «С». Далее второй идёт обратно и встречается с первым в точке «Д». Нам необходимо найти расстояние АД.
Разделим решение на две части.
Сначала вычислим на каком расстоянии от точки «А» будет находится первый в тот момент, когда второй дойдёт до точки «В». Время, за которое второй дойдёт до точки «В» будет равно (4,4)/3 часа. Первый за это же время пройдёт:

То есть, расстояние АС = 11/3 километра.
Теперь вторая часть задачи.
Теперь получается, что первый как бы выходит из точки «С» (на самом деле он продолжает своё движение) и идёт навстречу второму, который следует из точки «В» ему навстречу. Такая задача имеется на сайте, посмотрите её.
До встречи друг с другом они будут находится в движении равное количество времени, примем его за х часов. Тогда расстояние пройденное первым будет равно 2,5х км, а расстояние пройденное вторым будет равно 3х км.
То есть СД = 2,5∙х и ДВ = 3∙х. Сумма этих расстояний равна СВ, его мы можем без труда вычислить: СВ = АВ – АС = 4,4 – 11/3. Значит
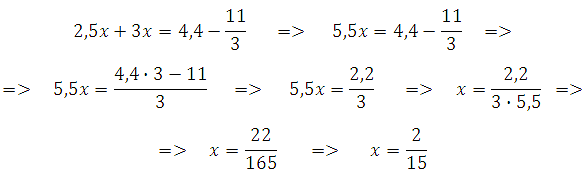
То есть, до их встречи в тоске «С», с того момента, когда второй начал движение в обратном направлении из точки «Д», пройдёт 2/15 часа.
Теперь, зная время, мы можем найти расстояния СД и ДВ и далее уже ответить на вопрос поставленный в задаче. Расстояние ДВ = 3∙(2/15) = 2/5=0,4 км.
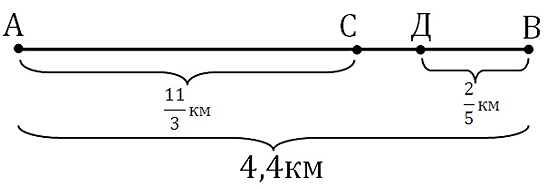
Таким образом, АД = АВ – ДВ = 4,4 – 0,4 = 4 километра.
Внимание! Теперь посмотрите как можно преобразить эту задачу и решить намного лаконичнее и быстрее: у нас в условии сказано, что два человека отправились одновременно из пункта А. Теперь представим, что второй вышел не из пункта А, а из противоположной точки Е, находящейся также в 4,4 км от опушки (точки В). Они идут встречу друг другу и сходятся в точке Д. Изменилась ли схема и суть задачи? Нет! Она осталась той же.
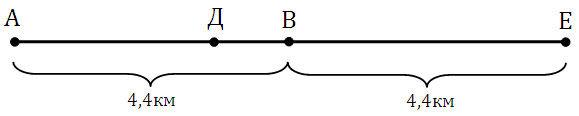
Но задача теперь решается в разы проще. Получается следующая картинка: расстояние между пунктами А и Е равно 8,8 км. Время которое прошло до встречи (точка Д) у них равное, обозначим его за х. Тогда шедший из А прошел 2,5х км, вышедший из Е прошёл 3х км
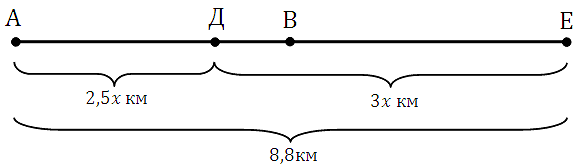 Уравнение:
Уравнение:
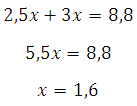
То есть они встретились через 1,6 часа. Таким образом, АД = 2,5∙1,6=4 км.
Ответ: 4
Теперь сравните — если знать подход к решению, то времени затрачивается всего ничего. Другие полезные «хитрости» найдете в книге «Самые хитрые задачи на ЕГЭ по математике»

На этом всё. Успеха Вам!
С уважением, Александр.
*Делитесь информацией о сайте в социальных сетях!
















А по мне все очень даже легко и понятно