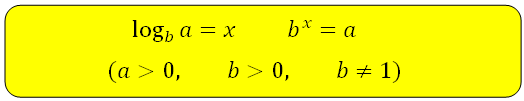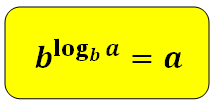Показательные уравнения. Как известно — в состав ЕГЭ входят простые уравнения. Некоторые мы уже рассмотрели – это логарифмические, тригонометрические, рациональные. Здесь представлены показательные уравнения.

В недавней статье мы поработали с показательными выражениями, посмотрите, будет полезно. Сами уравнения решаются просто и быстро. Требуется лишь знать свойства показателей степени и...  Об этом далее.

Перечислим свойства показателей степени:

Нулевая степень любого числа равна единице.

Далее:

Следствие из данного свойства:

Далее

    Иррациональные уравнения. Продолжаем рассматривать задачи части В ЕГЭ по математике. В этой рубрике уже опубликованы статьи «Тригонометрические уравнения», «Решение рациональных уравнений», «Логарифмические уравнения». Здесь мы разберём иррациональные уравнения.

Подобные примеры, как и большинство уравнений из данной части, справедливо можно назвать простыми заданиями на ЕГЭ. Необходимо уметь выполнять с уравнениями простейшие преобразования, в том числе «избавляться» от корня. Что делать, если в одной из частей у нас имеется выражение под знаком корня? Всё просто:

Если корень квадратный, то обе части уравнения возводим в квадрат.

Если корень третьей степени, то обе части возводим в третью степень.

Здесь работает следующее свойство: Далее

   Рациональные уравнения. Здравствуйте, друзья! В этой статье разберём рациональные уравнения, решим несколько примеров. Это один из самых простых типов уравнений, которые входят в состав экзамена по математике. Но небольшие особенности в выполнении этих заданий есть.

Для  решения достаточно провести безошибочно необходимые преобразования, и уметь решать квадратное уравнение. Напомню, что мы  можем:

1. Умножать и делить левую и правую части уравнения на одно и то же число или выражение.

2. Прибавлять к обеим частям уравнения или вычитать одно и то же число (выражение).

По-другому эта операция звучит так: перенос слагаемых, из левой части в правую и наоборот, при этом знак слагаемого изменяется на противоположный.

3. Можем возводить в квадрат и извлекать квадратный корень из обеих частей.

Квадратное уравнение (общий вид):

Далее

   Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно.  Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.

В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.  

Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.

Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.

Далее