![]()
В данной статье для вас основная теория по прямоугольному треугольнику, также мы с вами разберём несколько задач. На первый взгляд, число прототипов заданий, представленных в едином банке задач ЕГЭ, несколько пугает – их там более 300 (на момент написания этой статьи). Но практически все задания решаются в два, максимум в три действия. Многие даже в одно.
Представленные подходы к решению вполне применимы для других типов задач, в которых прямоугольный треугольник является частью другого (данного в условии) треугольника, например равнобедренного. Средства для их решения совершенно одни и те же. Постараюсь акцентировать внимание на базовых свойствах и основных методах, которые необходимы для решения.
Кстати, в большинстве пособий по подготовке к экзамену почему-то встречаются только примеры на решение прямоугольного треугольника, как будто других задач в этом разделе и не существует — странно, конечно. Теперь теория!
Прямоугольный треугольник — это треугольник, в котором один из углов прямой, то есть равен 90 градусов.
Вершина треугольника — точка, в которой сходятся две стороны треугольника.
Сторона треугольника — отрезок соединяющий две вершины треугольника.
Стороны прямоугольного треугольника имеют свои названия.
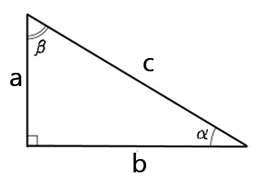
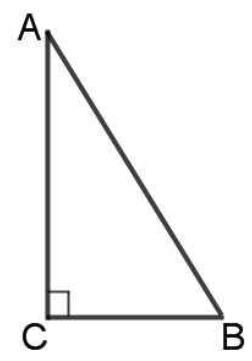
Гипотенуза — сторона прямоугольного треугольника, которая противоположна прямому углу. На рисунке.
Катеты — стороны прямоугольного треугольника, которые образуют прямой угол.
*Если длины всех трех сторон прямоугольного треугольника являются целыми числами, то такой треугольник называют Пифагоровым треугольником, а длины сторон образуют пифагорову тройку. Самый древний из известных Пифагоровых треугольников — Египетский треугольник, соотношение длин сторон которого 3:4:5.
Признаки равенства прямоугольных треугольников.
1. Признак равенства прямоугольных треугольников по двум катетам.
 Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
2. Признак равенства прямоугольных треугольников по катету и острому углу

Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Признак равенства по гипотенузе и острому углу

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
4. Признак равенства прямоугольных треугольников по катету и гипотенузе

Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Основное тригонометрическое тождество — знать его вы должны обязательно и вспомнить в любое время дня и ночи. Можно сказать что это основа для решения задач на прямоугольный треугольник. Формула «красивая» запоминается легко:

Из неё следуют следующие ...
Синус в квадрате и косинус в квадрате:

*Их запоминать не нужно, всегда сможете вывести путём простейших преобразований, которые используете в уравнениях.
**Когда речь идёт об использовании этой формулы для решения прямоугольного треугольника, то перед корнем ставиться знак «+», так как углы в этом треугольнике острые, а мы знаем, что синус и косинус острого угла имеет положитльный знак.
Так же из неё получаем две другие необходимые формулы путём деления на квадрат синуса и квадрат косинуса:
Учить эти формулы не нужно, вы всегда их сможете вывести. Признаюсь сам я до сих пор их не выучил, когда нужны, вывожу их, правда устно.
Что ещё? Формулы тангенса и котангенса (выучить не сложно, выводить их будет длительнее, чем вспоминать, они просты):
Понятие синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике.
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла. Катеты — стороны, лежащие напротив острых углов.
Катет а, лежащий напротив угла альфа, называется противолежащим (по отношению к углу альфа). Другой катет b, который лежит на одной из сторон угла а, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
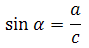 Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
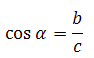 Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
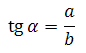 Другое (равносильное) определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
Другое (равносильное) определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
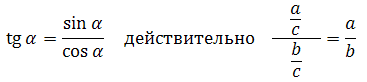 Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Без знания представленных определений задачи не решить. Нужно выучить!!! Проработайте определения многократно. Основная проблема в том, что учащиеся спустя время всё-таки путают в определениях синуса и косинуса — то ли прилежащий катет относится к гипотенузе, то ли противолежащий; в определениях тангенса и котангенса — то ли прилежащий катет относится к противолежащему, то ли наоборот.
По этому поводу обязательно будет статья, как быстро вспомнить эти отношения без ошибки. Постараюсь не затягивать! Вобще, темы для статей у меня в голове прибывают в геометрической прогрессии. Хочется Вам столько всего выдать, но времени маловато.
Ещё факт, который советую запомнить: синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём. И наоборот: косинус одного острого угла в прямоугольном треугольнике равен синусу другого.
Итого: основные соотношения для синуса, косинуса, тангенса и котангенса, которые пригодятся при решении задач:

 Вывод: зная любые две стороны, мы можем найти третью сторону треугольника. Мой вам совет — каким бы не стоял вопрос, но если в задаче на прямоугольный треугольник даны две стороны, сразу же находите третью, пригодится однозначно. Зная все три стороны, вы без труда найдёте значение любой тригонометрической функции (и любой угол).
Вывод: зная любые две стороны, мы можем найти третью сторону треугольника. Мой вам совет — каким бы не стоял вопрос, но если в задаче на прямоугольный треугольник даны две стороны, сразу же находите третью, пригодится однозначно. Зная все три стороны, вы без труда найдёте значение любой тригонометрической функции (и любой угол).

В треугольнике АВС угол С равен 900,  . Найдите tg A.
. Найдите tg A.

Если в условии нет данных о сторонах и углах, а есть только тригонометрические функции, то пользуйтесь формулами:

Сразу видно, что можно использовать формулу:

Остаётся из основного тригонометрического тождества sin2A + cos2A = 1 найти cosA:

Таким образом:

Ответ: 0,25

Дан прямоугольный треугольник АВС, угол C равен 900,  . Найдите tg В.
. Найдите tg В.

Здесь необходимо найти тангенс другого острого угла. Как быть?
Воспользуемся формулой тангенса:

Мы знаем, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла, и наоборот, то есть:
![]()
Найдём sin B.
Из основного тригонометрического тождества sin2A + cos2A = 1 найдём cos A:

Значит

Таким образом:

Ответ: 0,25

Дан прямоугольный треугольник АВС, угол C равен 900, tg A = 7/24. Найдите sin A.

Используем формулу:

Из неё мы без труда найдём cos2A, а далее используя формулу основного тригонометрического тождества sin2A + cos2A = 1, сможем определить синус:

Вычислим sin A:

Ответ: 0,28
*Обратите внимание, что мы вычислили не косинус, а квадрат косинуса, так как далее для вычислений нам нужен именно квадрат.

Дан прямоугольный треугольник АВС, C равен 900, АВ = 8, sin A = 0,5. Найдите BC.

Здесь нам дана сторона (гипотенуза) и синус угла.
Задача в одно действие, используется определение синуса:

Ответ: 4

Дан прямоугольный треугольник АВС, C равен 900, АВ = 7, tg = . Найдите ВC.
. Найдите ВC.

В данной задаче через функцию тангенса мы можем выразить только катеты, но они нам неизвестны. Поэтому выразим её через функцию косинуса. Далее по определению косинуса, мы сможем найти АС, а затем по теореме Пифагора найдём ВС. Итак:
Следовательно:

По определению косинуса cos A = AC/АВ, значит можем найти АС:

Далее по теореме Пифагора вычислим ВС:

Таким образом, ВС = 4.
Ответ: 4

Дан прямоугольный треугольник АВС, угол C равен 900, АС = 24, ВС = 7. Найдите sin A.

Мы уже говорили, что если в задаче известны две стороны, то лучше сразу найти третью сторону по теореме Пифагора. Зная все три стороны в прямоугольном треугольнике, мы всегда без труда найдём значение любой тригонометрической функции любого угла.
По теореме Пифагора:

По определению синуса:

Ответ: 0,28

Дан прямоугольный треугольник АВС, угол C равен 900,  , sin A = 11/14. Найдите AB.
, sin A = 11/14. Найдите AB.

По определению косинуса cos A = АС/АВ, значит:

Сторона АС нам известна, найдём cos A.
Из основного тригонометрического тождества:

Таким образом:

Ответ: 28
Если вы найдёте более рациональные пути решения подобных задач, это будет замечательно, я лишь преследовал цель показать вам основные приёмы и необходимые формулы. Способов решения каждой подобной задачи на самом деле, не менее трёх.
Решите самостоятельно:
Посмотреть решения: 27217, 27219, 27220, 27226, 27228, 27231, 27232, 27236, 27240, 27243, 27251, 27246, 27255.
В будущем мы так же будем разбирать и другие задачи на решение прямоугольного треугольника отличные от предоставленных, но теории уже касаться не буду. Надеюсь, материал был вам полезен.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.








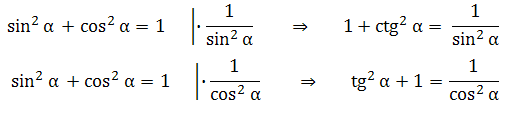
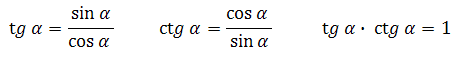
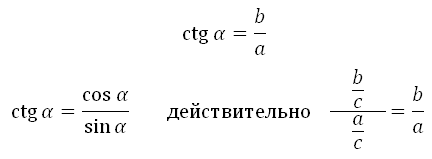
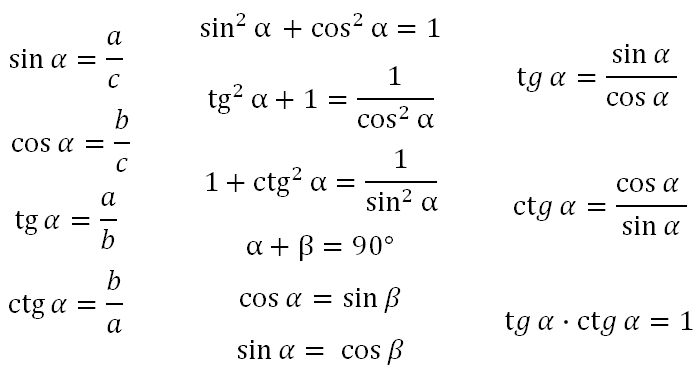
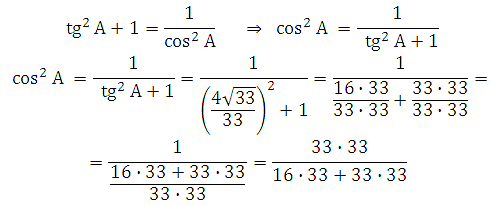









Полезно! Спасибо!!!
Ольга, пожалуйста , пользуйтесь на здоровье!!!
Спасибо, обязательно ученикам расскажу.
Наталья, пожалуйста!
Спасибо за материалы. Очень удачно скомплектованы, удобны в использовании.Моим ученикам тоже нравятся Ваши труды.
Александр,как в последней задаче из 75 мы получили 5 корень из 3?
75 это 25 умножить на 3. Корень из 25 равен пяти, корень из трёх остаётся. Используется свойство корней вторая строчка
matematikalegko.ru/shkoln.../korni-i-stepeni
Александр, помогите пожалуйсто, никак не удаётся решить задачу... В треугольнике АВС АС=ВС, АВ=30, сosА=5\13. Найдите высоту СН
Треугольник равнобедренный, АВ это основание, строим СН (соединяем вершину С с серединой основания АВ). Из треугольника АСН зная cosА и АН (30/2=15) можем найти АС. А далее по теореме Пифагора находим катет СН из треугольника АСН.
Здравствйте!В пятой задаче условия не совпадают с решением,Условие: В треугольнике ABC угол C равен 900, АВ = 7, tg = 4 корней из 17/корень из 17 . Найдите ВC.
А в решении tg = 4 корней из 33/корень из 33
Анастасия, спасибо. ваши поправки ценны! В условии ошибка,исправлено ))
Помогите решить.
В треугольнике АВС sinA=трем пятым.найти ас.