Часы со стрелками показывают

В этой публикации рассмотрим задачу: в условии говорится о движении стрелок часов. Это задача на движение. Рассмотрим разные подходы к решению, будет и такой, при применении которого такие задания будете решать не более чем за одну минуту. Приступим! Алгебраический подход к решению:

99600. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

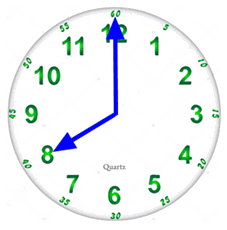
За один час минутная стрелка проходит один круг, то есть скорость хода стрелки будет ОДИН круг в час. Часовая за час проходит 1/12 круга, то есть её скорость будет 1/12 круга в час. Обозначим время которое идут стрелки переменной «t».

Тогда до встречи стрелки пройдут:

*В данном случае у нас роль расстояния играет круг циферблата .

Отставание минутной от часовой составляло 8 часов – это 2/3 круга. То есть получается, что разность между пройденными «расстояниями» составляет 2/3.

*Если вам удобнее занести данные в таблицу, то:

Можем записать:

Итак, в первый раз стрелки пересекутся через 8/11 часа.

Пусть во второй раз они пересекутся через время z. Минутная стрелка пройдет расстояние 1∙z, а часовая (1/12)∙z, причем минутная стрелка пройдет на один круг больше. Запишем  уравнение:

Значит через 12/11 часа стрелки пересекутся во второй раз, еще через 12/11 часа — в третий, и еще через 12/11 часа — в четвертый.

Значит если старт был в 8.00, то в четвертый раз стрелки пересекутся через:

Ответ: 240

*Если развита интуиция и логическое мышление, то ответ в данной задаче можно дать сразу по прочтении условия. Смотрите: первый раз стрелки пересекутся в девятом часу, второй раз в десятом, третий в одиннадцатом, а четвёртый ровно в двенадцать, то есть через 4 часа (240 минут).

Ещё задача. Часы со стрелками показывают 4 часа 45 минут. Через сколько минут минутная стрелка в седьмой  раз поравняется с часовой?

Отставание минутной от часовой составляло 7 часов 45 минут, то есть 7 плюс ¾ часа. Переведём в часть круга. Воспользуемся пропорцией:

По аналогии с предыдущей задачей:

Итак, в первый раз стрелки пересекутся через 31/44 часа.

Пусть во второй раз они пересекутся через время z, тогда:

Значит через 12/11 часа стрелки пересекутся во второй раз, еще через 12/11 часа — в третий и так далее … Значит если старт был в 4:45, то в седьмой раз стрелки пересекутся через:

В минутах это 7∙60+15=435.

Ответ: 435.

Небольшой итог! При решении необходимо:

— определить отставание минутной стрелки от часовой в частях круга,

— далее вычислить через какое время  стрелки пересекутся в первый раз,

— затем определить время пересечения стрелок во второй и последующие разы (его можно просто запомнить  12/11 часа – это время через которое стрелки встречаются «от пресечения до пересечения»),

— далее вычислить общее время.

Но! Теперь СПЕЦ-совет для  решения такой задачи на самом экзамене. Ведь не секрет, что время имеет большую ценность и разбрасываться им на экзамене просто преступно ))).

Способ второй (простая логика)! Решаем за минуту!

Давайте разберём предыдущую задачу. Время 4 часа 45 минут.

Первый раз стрелки пересекутся между пятью и шестью часами,  то есть в шестом часу, второй в седьмом часу, третий раз в восьмом, четвёртый в девятом, пятый в десятом, шестой в одиннадцатом, седьмой в 12 часов.

То есть времени пройдёт 7 часов 15 минут, 7∙60+15=435.

Таким образом, просто загибая пальцы на руке вы решаете задачу за одну минуту без лишних вычислений.

Теперь ряд задач на часы со стрелками для отработки.

На часах 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Время 3 часа. Первый раз стрелки пересекутся в четвёртом часу, второй в пятом часу, третий раз в шестом, четвёртый в седьмом, пятый в восьмом, шестой в девятом, седьмой в десятом, восьмой в одиннадцатом, девятый в 12 часов.

То есть пройдёт 9 часов,  9∙60=540 минут.

Время 11 часов 40 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Первый раз стрелки пересекутся 12 часов, то есть через 20 минут.

Время 6 часов 45 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Первый раз стрелки пересекутся в восьмом часу, второй в девятом, третий раз в десятом, четвёртый в одиннадцатом  в 12 часов.

То есть времени пройдёт от 6:45 до 12 пройдёт 5 часов 15 минут, 5∙60+15=315 минут.

Время 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Первый раз стрелки пересекутся в восьмом часу, второй в девятом, третий раз в десятом, четвёртый в одиннадцатом  в 12 часов.

То есть времени пройдёт от 6:35 до 12 пройдёт 5 часов 25 минут, 5∙60+25=325 минут.

Время 2 часа ровно. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Первый раз стрелки пересекутся в третьем часу, …. , десятый в 12 часов.

То есть времени пройдёт 10 часов, 10∙60=600 минут.

Время 8 часов 20 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Первый раз стрелки пересекутся в девятом часу, второй в десятом, третий раз в одиннадцатом, четвёртый в 12 часов.

То есть времени от 8:20 до 12 пройдёт 3 часов 40 минут, 3∙60+40=220 минут.

Время 2 часа 5 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Первый раз стрелки пересекутся в третьем часу, …. ,  десятый в 12 часов.

То есть  пройдёт 9 часов 55 минут, 9∙60+55=595 минут.

Ответ: 595

Как видите, такие задачи можно решать устно. Заметили что все они составлены таким образом, что последнее пересечение стрелок попадает на 12:00? Иначе в ответе нельзя получить целое число или конечную десятичную дробь (это требование и условие для задач экзамена). Только через следующие 12 часов (это ещё плюс 11 пересечений).

На этом всё!

С уважением, Александр.

*Делитесь информацией в социальных сетях