Вычислить угол между векторами. В этой публикации хочу вам показать один способ определения угла между двумя векторами. В условии для каждого из векторов задаются координаты начала и конца. Векторы могут быть построены на координатной плоскости или без того. Конечно же, данную задачу обычно (и это естественно) решают применяя формулу скалярного произведения векторов, и такой подход был показан в этой статье.
Но если пофантазировать и представить, что вдруг вы напрочь забыли эту формулу или вообще в решении задач с векторами как-то давно не практиковались, то на помощь может прийти нижеизложенный способ. Это вполне достойная альтернатива. Чем у вас будет больше «инструментов» в запасе, тем лучше.

Найти угол между векторами. Ответ дать в градусах.

Идея очень простая: мы строим треугольник (соединяем концы векторов) и далее используем способ изложенный в этой статье. Его суть такова – в полученном треугольнике вычисляем стороны и для далее вычисления искомого угла используем теорему косинусов.
Приступим! Строим треугольник, далее описываем около него прямоугольник. Затем прямо на эскизе обозначаем длины катетов в образовавшихся прямоугольных треугольниках:
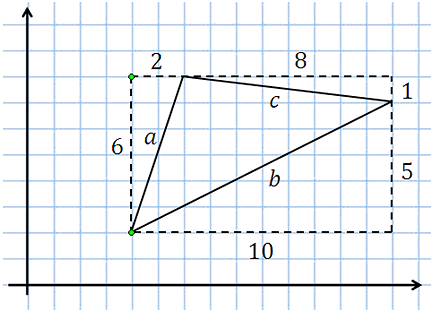
Вычисляем стороны. По теореме Пифагора:
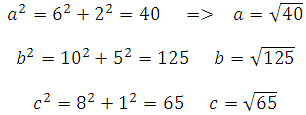
Теорема косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
![]()
Вычисляем угол:
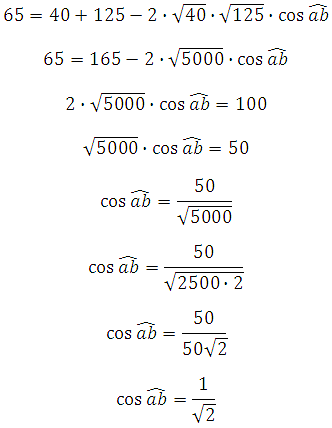
Таким образом, угол между векторами равен 45 градусам.
Ответ: 45
Сама формула:
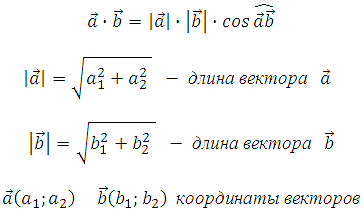
Известна следующая формула.
Скалярным произведением векторов на плоскости в прямоугольной системе координат называется число равное сумме произведений соответствующих координат векторов.
![]()
Значит:
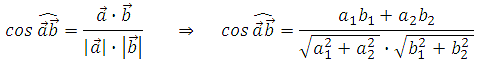
Вычислим координаты векторов:
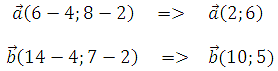
Подставим их в формулу:
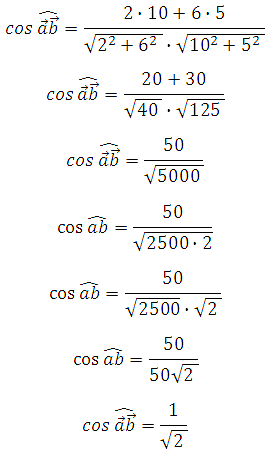
Таким образом, угол между векторами равен 45 градусам.
Ответ: 45
*Если векторы будут расположены на координатной плоскости не касаясь друг друга, то один из них всегда можно сдвинуть параллельным переносом и далее уже действовать как описано выше.
**Если они будут построены схематично на координатной плоскости, а не на листе в клетку и при этом будут указаны координат концов, то треугольник построить несложно.
С уважением, Александр.
В школе урок математики. Учитель:
— Петя, назови двузначное число!
— Сорок шесть.
— Теперь поменяй местами цифры и скажи, что получилось.
— Не знаю...
— Садись, два! Вовочка, назови двузначное число!
— Тридцать три, и можете начинать свои фигли-мигли!
*Делитесь информацией в социальных сетях!
















Спасибо за идею. Надеюсь пригодится.
Угол проще вычислить как tg (a-b)=(tga-tgb)/(1+tgatgb)=(3-0.5)/(1+3*0.5)=1