Решить уравнение sin (3Пи/2-2x)=sinx

  Здравствуйте, Дорогие друзья! В данной статье мы с вами рассмотрим решение тригонометрического уравнения, и найдём корни принадлежащие определённому (заданному) отрезку. Подобный пример мы уже рассмотрели в предыдущей статье данной рубрики. Но в этом примере мы разберём другой способ определения  корней на отрезке.

Дано уравнение

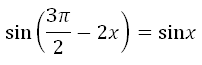
а) Решите уравнение.
б) Укажите корни уравнения, принадлежащие отрезку

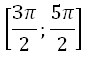
Решение:

а) Используем формулу приведения для синуса и формулу косинуса двойного угла:

Привели уравнение к квадратному. Производим замену переменной, обозначим sin x = t.

Решая квадратное уравнение  2t² – t – 1 = 0, получим:

Это простейшие тригонометрические уравнения.

Решая  sin x = 1,  получим:

Решая sin x = –½,  получим:

Итак, мы получили корни:

б) С помощью единичной окружности отберём корни на отрезке

Без расчётов, визуально сходу определить корни принадлежащие отрезку может далеко не каждый. Для этого необходима большая практика и отличное «понимание» тригонометрической окружности. Рассмотрим способ, при использовании которого, вы безошибочно определите корни на заданном интервале. Переведём  радианы в  градусы. Так  как Пи  радиан  это 180 градусов, то отрезок

в (градусах) будет выглядеть следующим образом: [270⁰;450⁰]. Отберём  корни.

Суть подхода такова: мы берём произвольные коэффициенты k, подставляем в каждый из корней и вычисляем. Получаем корни (углы) и смотрим – попадают ли они в интервал. Те, которые попадают мы отмечаем как верный ответ.

При k = 1:

При k = 2:

При k = 3  и  далее можно не проверять, так как уже видно, что при этом значении k углы будут находиться вне пределов интервала.

Таким образом, отрезку [270⁰;450⁰] принадлежат корни  450⁰  и  330⁰ в радианах это

Возникает вопрос: какие «произвольные»  коэффициенты k брать?

Ответ прост: в пределах от –3 до 3, так как границы заданного интервала в подобных заданиях обычно лежат «недалеко» от нуля. Для начала берите k = 0, затем по полученным значениям корней поймете какие коэффициенты брать, положительные или отрицательные.

Конечно, данный способ совершенным не назовёшь, кому-то наиболее понятен подход изложенный в уже указанной выше статье. Но он, безусловно, позволяет находить верное решение. Да и в градусной мере оценивать принадлежность угла указанному интервалу многим удобнее.

Кстати, если сравнивать объём вычислений представленного способа и описанного в уже указанной статье (см. ссылку выше), то он практически одинаков.

На этой странице вы можете посмотреть примеры уравнений.

На этом всё. Успехов Вам!