Площадь многоугольника

Площадь многоугольника. Друзья!  К вашему вниманию пару задачек с многоугольником и вписанной в него окружностью. Существует формула, которой связывается радиус указанной окружности и периметр с площадью такого многоугольника. Вот она:

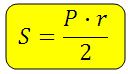
Как выводится эта формула? Просто!

Имеем многоугольник и вписанную окружность. *Рассмотрим вывод на примере пятиугольника. Разобьём его на треугольники (соединим центр окружности и вершины отрезками). Получается, что у каждого треугольника основание является стороной многоугольника, а высоты образованных треугольников равны радиусу вписанной окружности:

Используя формулу площади треугольника можем записать:

Вынесем общие множители:

Уверен, сам принцип вам понятен.

*При выводе формулы количество сторон взятого многоугольника не имеет значения. В общем виде вывод формулы выглядел бы так:

*Дополнительная информация!

Известна формула радиуса окружности вписанной в треугольник

Не трудно заметить, что она исходит из полученной нами формулы, посмотрите (a,b,c – это стороны треугольника):

27640. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.

Вычисляем:

Ответ: 30

Ещё пара задач с многоугольниками.

27930. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 54⁰. Найдите n.

Если угол между радиусом окружности и стороной многоугольника равен 54⁰, то угол между сторонами многоугольника будет равен 108⁰. Тут необходимо вспомнить формулу угла правильного многоугольника:

Остаётся подставить в формулу значение угла и вычислить n:

Ответ: 5

27595. Периметры двух подобных многоугольников относятся как 2:7. Площадь меньшего многоугольника равна 28. Найдите площадь большего многоугольника.

Здесь нужно вспомнить о том, что если линейные размеры фигуры увеличивается в k раз, то площадь фигуры увеличивается в k² раз. *Свойство подобия фигур.

Периметр большего многоугольника больше периметра меньшего в 7/2 раза, значит площадь увеличилась в (7/2)² раза.  Таким образом, площадь большего многоугольника равна:

Ответ: 343

27639. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.

Посмотреть решение

27641. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.

Посмотреть решение

27595. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.

Ответ: 50

Всего доброго! Учитесь с удовольствием!

С уважением, Александр.