В прошлой статье мы с вами разобрали, как быстро восстановить в памяти формулы площади сектора круга, длины дуги окружности, площади сегмента круга. Первые две формулы как раз нам понадобятся для решения ряда заданий связанных с кругом.
Рассмотренные ниже задачи на первый взгляд могут показаться не очень простыми, но зная оговоренные выше формулы и используя простую логику решение осуществите без труда. Примеры не представляют никакой сложности. Необходимо помнить сами формулы (или быстро восстановить их в памяти), и путём простейших преобразований выразить радиус или центральный угол. Рассмотрим задачи:
Найдите площадь круга, длина окружности которого равна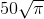 
.
Формула площади круга:
Формула длины окружности:
Для того, чтобы найти площадь круга, необходимо найти радиус круга, его мы можем найти используя формулу длины окружности, подставляем данное в условии значение:
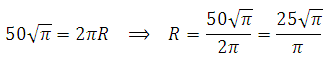
Подставим найденный радиус в формулу площади круга и найдём её:
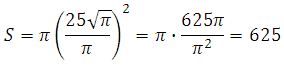
Ответ: 625
Площадь круга равна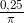 
. Найдите длину его окружности.
Формула площади круга:
Формула длины окружности:
Это задача обратная предыдущей. Для нахождения длины окружности необходимо используя формулу площади круга найти его радиус. Сделаем это:
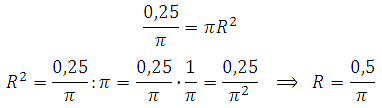
Значит длина окружности равна:
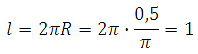
Ответ: 1
Найдите площадь сектора круга радиуса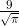 
, центральный угол которого равен 900.
Формула площади круга:
Сектор круга с центральным углом 90 градусов составляет четвёртую часть от целого круга. Вообще, площадь сектора круга определяется по формуле:
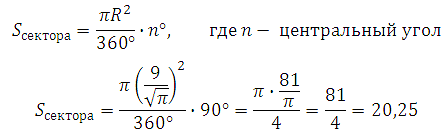
Ответ: 20,25
Найдите площадь сектора круга радиуса 41, длина дуги которого равна 2.
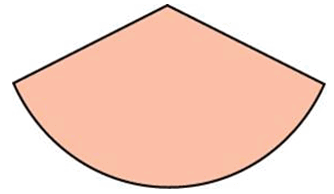
Площадь сектора круга определяется по формуле:
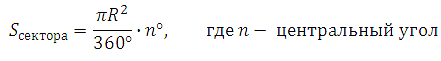
Длина дуги сектора:
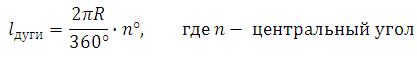
Для нахождения площади сектора нам необходимо найти центральный угол n. Его мы можем найти используя формулу длины дуги:
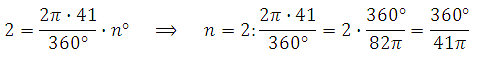
Подставляем:
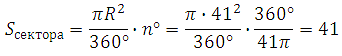
Ответ: 41
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны и
.
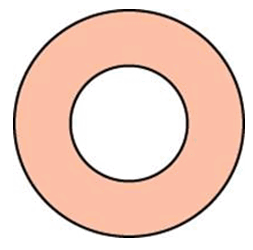
Формула площади круга:
Нам необходимо вычислить площадь большего круга и площадь меньшего круга, найти разность. Эта разность будет являться площадью кольца:
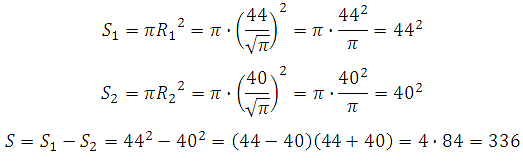
Ответ: 336
Найдите центральный угол сектора круга радиуса , площадь которого равна 375. Ответ дайте в градусах.
Площадь сектора круга определяется по формуле:
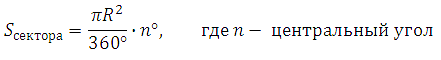
Подставим известные величины:
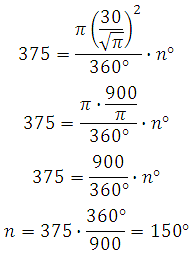
Ответ: 150
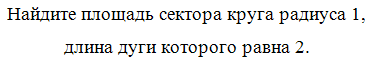
На этом всё. В данной рубрике мы продолжим рассматривать задачи, не пропустите!Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
