Объем правильной шестиугольной пирамиды

Задачи с пирамидами. В данной статье продолжим рассматривать задачи с пирамидами. Их нельзя отнести к какому-то классу или типу заданий и дать общие (алгоритмы) рекомендации для решения. Просто здесь собраны оставшиеся задачи, не рассмотренные ранее.

Перечислю теорию, которую необходимо освежить в памяти перед решением: формула объёма пирамиды, свойства подобия фигур и тел, свойства правильных пирамид, теорема Пифагора, формула площади треугольника (в этой статье она вторая). Рассмотрим задачи:

От треугольной пирамиды, объем которой равен 80, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Объём пирамиды равен одной трети произведения площади её основания и высоты:

Данные пирамиды (исходная и отсечённая) имеют общую высоту, поэтому их объемы соотносятся как площади их оснований. Средняя линия от исходного треугольника отсекает треугольник площадь которого в четыре раза меньше, то есть:

Подробнее об этом можно посмотреть здесь.

Это означает, что объём отсечённой пирамиды будет в четыре раза меньше.

Таким образом, он будет равен 20.

Ответ: 20

*Посмотрите решение аналогичной задачи,  использована формула площади треугольника.

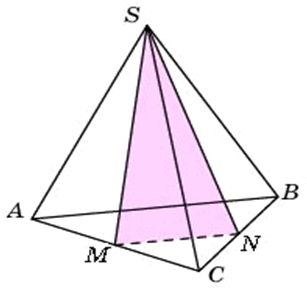
Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.

Постоим пирамиду, обозначим вершины. Отметим на ребре AS точку Е, так чтобы  AE была в два раза больше ES (в условии сказано, что ES относится к AE как 1 к 2), и построим указанную плоскость проходящую, через ребро АС и точку Е:

Проанализируем объём какой пирамиды будет больше:  EABC или SEBC?

*Объём пирамиды равен одной трети произведения площади её основания и высоты:

Если рассмотреть две полученные пирамиды и в обеих принять за основание грань ЕВС, то становится очевидно, то объём пирамиды АЕВС будет больше объёма пирамиды SEBC. Почему?

Расстояние от точки А до плоскости ЕВС  больше чем расстояние от точки S. А это расстояние играет у нас роль высоты. 

Итак, найдём объём пирамиды ЕАВС.

Объём исходной пирамиды нам дан, основание у пирамид SАВС и ЕАВС общее. Если мы установим соотношение высот, то без труда сможем определить объём.

Из отношения отрезков  ES и AE следует, что АЕ равно две третьих ES. Высоты пирамид SАВС и ЕАВС находятся в такой же зависимости - высота пирамиды ЕАВС будет равна 2/3 высоты пирамиды SАВС.

Таким образом, если

То

Ответ: 10

Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.

В правильной пирамиде вершина проецируется в центр основания. Выполним дополнительные построения:

Найти боковое ребро мы можем из прямоугольного треугольника SOC. Для этого нужно знать SO и ОС.

SO это высота пирамиды, её мы можем вычислить используя формулу объёма:

Вычислим площадь основания. это правильный шестиугольник со стороной равной 1. Площадь правильного шестиугольника равна площади шести равносторонних треугольников с такой же стороной, подробнее об этом изложено здесь (п.6), итак:

Значит

ОС = ВС = 1, так как в правильном шестиугольнике отрезок соединяющий его центр с вершиной равен стороне этого шестиугольника.

Таким образом, по теореме Пифагора:

Ответ: 7

Объем указанного многогранника равен разности объемов исходного тетраэдра V₀ и четырех равных тетраэдров, каждый из которых получается отсечением плоскостью, проходящей через середины  рёбер, имеющих общую вершину:

Определим, чему равен объём отсеченного тетраэдра.

Отметим, что исходный тетраэдр и «отсечённый» тетраэдр являются подобными телами. Известно, что отношение объёмов подобных тел равно k³, где k - коэффициент подобия. В данном случае он равен 2 (так как все линейные размеры исходного тетраэдра в два раза больше соответствующих размеров отсечённого):

Вычислим объём отсечённого тетраэдра:

Таким образом, искомый объём будет равен:

Ответ: 100

Первый способ:

Искомая поверхность состоит из 8 равносторонних треугольников со стороной, вдвое меньшей ребра исходного тетраэдра. Поверхность исходного тетраэдра состоит из 16-ти таких треугольников (на каждой из 4 граней тетраэдра по 4 треугольника), поэтому искомая площадь равна половине площади поверхности данного тетраэдра и равна 60.

Второй способ:

Так как известна площадь поверхности тетраэдра, то мы можем найти его ребро, затем определить длину ребра многогранника и далее вычислить площадь его поверхности.

Площадь поверхности тетраэдра состоит из четырёх равных по площади правильных треугольников. Пусть сторона такого треугольника (ребро тетраэдра) равна а, тогда можем записать:

Ребра многогранника равны его половине ребра тетраэдра, то есть:

*Они проходят через середины рёбер тетраэдра.

Многогранник имеет восемь равных граней являющихся правильными треугольниками, значит его площадь поверхности будет равна:

*Данное решение алгебраическое и рациональным его назвать никак нельзя, представлено как альтернативный вариант.

Ответ: 60

27115. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Посмотреть решение

27175. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

Посмотреть решение

27214. Объем тетраэдра равен 1,9. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.

Посмотреть решение

На этом всё. Успеха Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.