Правильная четырехугольная пирамида

Продолжаем рассматривать задачи входящие в ЕГЭ по математике. Мы уже исследовали задачи, где в условии дан составной многогранник и требуется найти расстояние между двумя данными точками либо угол.  

Пирамида — это многогранник, основание которого является многоугольником, остальные грани — треугольники, при чём они имеют общую вершину.

Правильная пирамида — это пирамида в основании которой лежит правильный многоугольник, а его вершина проецируется в центр основания.

Правильная четырехугольная пирамида — снованием является квадрат.Вершина пирамиды проектируется в точку пересечения диагоналей основания (квадрата).

ML — апофема
∠MLO — двугранный угол при основании пирамиды
∠MCO — угол между боковым ребром и плоскостью основания пирамиды

В этой статье мы с вами рассмотрим задачи на решение правильной пирамиды. Требуется найти какой-либо элемент, площадь боковой поверхности, объём, высоту. Разумеется, необходимо знать теорему Пифагора, формулу площади боковой поверхности пирамиды, формулу для нахождения объёма пирамиды.

В статье «Общий обзор. Формулы стереометрии!»  представлены формулы, которые необходимы для решения задач по стереометрии. Итак, задачи:

В правильной четырехугольной пирамиде SABCD точка O  — центр основания, S вершина, SO = 51,  AC = 136. Найдите боковое ребро SC.

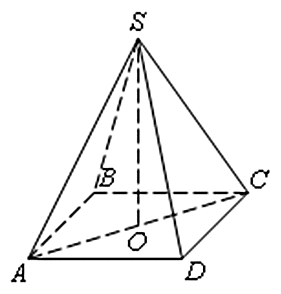
В данном случае в основании лежит квадрат. Это означает, что диагонали AC и BD равны, они пересекаются и точкой пересечения делятся пополам. Отметим, что в правильной пирамиде высота опущенная из её вершины проходит через центр основания пирамиды. Таким образом, SO является высотой, а  треугольник SOC прямоугольный. Тогда по теореме Пифагора:

Как извлекать корень из большого числа описано здесь.

Ответ: 85

Решите самостоятельно:

В правильной четырехугольной пирамиде SABCD  точка O  — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.

Посмотреть решение 

В правильной четырехугольной пирамиде SABCD точка O  — центр основания, S вершина, SC = 5, AC = 6. Найдите длину отрезка SO.

Посмотреть решение 

В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина,  SO = 4, SC = 5. Найдите длину отрезка AC.

Посмотреть решение

В правильной треугольной пирамиде SABC  R — середина ребра BC, S  — вершина. Известно, что AB = 7, а SR = 16. Найдите площадь боковой поверхности.

Площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему (апофема это высота боковой грани правильной пирамиды, проведённая из её вершины):

Или можно сказать так: площадь боковой поверхности пирамиды равна сумме площадей трёх боковых граней. Боковыми гранями в правильной треугольной пирамиде являются равные по площади треугольники. В данном  случае:

Ответ: 168

Решите самостоятельно:

В правильной треугольной пирамиде SABC  R — середина ребра BC, S  — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.

Посмотреть решение

В правильной треугольной пирамиде SABC R  — середина ребра BC, S  — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SR.

Посмотреть решение

В правильной треугольной пирамиде SABC  L  — середина ребра BC, S  — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.

Посмотреть решение

В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 25, объем пирамиды равен 100. Найдите длину отрезка MS.

Основание пирамиды — равносторонний треугольник. Поэтому M является центром основания, а MS — высотой правильной пирамиды SABC. Объем пирамиды SABC равен:

Ответ: 12

Решите самостоятельно:

В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.

Посмотреть решение

В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.

Посмотреть решение

В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Объем пирамиды равен 1, MS = 1. Найдите площадь треугольника ABC.

Посмотреть решение

На этом закончим. Как видите, задачи решаются в одно-два действия. В будущем рассмотрим  с вами другие задачи из данной части, где даны тела вращения, не пропустите!

Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.