Касательная к окружности. Вычисление углов!

   Касательная к окружности. Дорогие друзья!  В состав базы заданий ЕГЭ по математике входит группа задач, где в условии речь идёт о касательной и ставится вопрос о вычислении угла. Задачи эти чрезвычайно просты. Немного теории:

Что такое касательная к окружности?

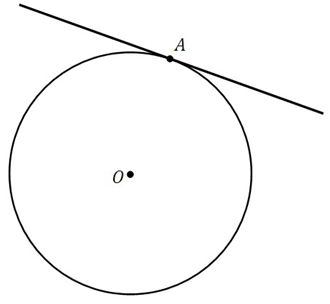
Важно помнить одно основное свойство касательной:

В представленных задачах используются ещё два свойства связанные с углами:

1. Сумма углов четырёхугольника равна 360⁰, подробнее здесь.

2. Сумма острых углов прямоугольного треугольника равна 90⁰.

Рассмотрим задачи:

27879. Через концы A и B дуги окружности в 62⁰ проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

Сказано, что градусная мера дуги АВ соответствует 62 градусам, то есть угол АОВ равен 62⁰.

Первый способ.

Так как ВС и АС касательные, то по свойству касательной:

Известно, что сумма углов в четырёхугольнике равна  360⁰.

В четырёхугольнике ОАСВ нам известны три угла, можем найти четвёртый:

Второй способ.

В треугольнике АВС мы можем найти углы АВС и ВАС. Воспользуемся свойством касательной.

Так как ВС это касательная, то угол ОВС равен 90⁰, значит:

Аналогично

В равнобедренном треугольнике АОВ:

Значит

По теореме о сумме углов треугольника:

Ответ: 118⁰

27880. Касательные CA и CB к окружности образуют угол ACB, равный 122⁰. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Задача обратная предыдущей. Необходимо найти угол АОВ.

Так как ВС и АС касательные, то по свойству касательной:

Известно, что сумма углов в четырёхугольнике равна  360⁰.

В четырёхугольнике ОАСВ нам известны три угла, можем найти четвёртый:

Ответ: 58

27882. Угол ACO равен 28⁰, где O  — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Градусная величина дуги соответствует углу  АОС. То есть задача сводится к нахождению угла АОС в прямоугольном треугольнике ОСА. Треугольник является прямоугольны, так как АС касательная, а угол между касательной и радиусом проведённым к точке касания равен 90 градусам.

По свойству прямоугольного треугольника сумма его острых углов равна 90⁰, значит:

Ответ: 62

27883. Найдите угол ACO, если его сторона CA касается окружности, O  — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116⁰. Ответ дайте в градусах. 

Сказано, что дуга AD окружности, заключенная внутри угла АСО, равна 116⁰, то есть угол DOA равен 116⁰. Треугольник ОСА прямоугольный.

Углы АОС и DOA  смежные, то есть их сумма равна 180⁰, значит:

Искомый угол равен:

Ответ: 26

27884. Угол ACO равен 24⁰. Его сторона CA касается окружности. Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах. Ответ: 114 

27878. Угол между хордой AB и касательной BC к окружности равен 32⁰. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах. Ответ: 58

27877. Хорда AB стягивает дугу окружности в 92⁰. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Посмотреть решение

27881. Найдите угол ACO, если его сторона CA касается окружности, O  — центр окружности, а угловая мера дуги  AB, заключенной внутри этого угла, составляет 64^о. Ответ дайте в градусах.

Посмотреть решение

На этом всё. Успеха вам!

С уважением, Александр Крутицких 

Отец смотрит дневник сына.
— Ну, что это у тебя за оценки, одни тройки, ни одной пятерки и четверки!
— Папа, так ведь и школа у нас средняя!

P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.