![]()
Составить пропорцию. В этой статье хочу поговорить с вами о пропорции. Понимать, что такое пропорция, уметь составлять её – это очень важно, она действительно спасает. Это вроде бы маленькая и незначительная «буковка» в большом алфавите математики, но без неё математика обречена быть хромой и неполноценной. Для начала напомню, что такое пропорция. Это равенство вида:

что тоже самое (это разная форма записи).
Пример:

Говорят – один относится к двум также, как четыре относится к восьми. То есть это равенство двух отношений (в данном примере отношения числовые).
Основное правило пропорции:
a:b=c:d
произведение крайних членов равно произведению средних
то есть
a∙d=b∙c
*Если какая-либо величина в пропорции неизвестна, ее всегда можно найти.
Если рассматривать форму записи вида:

то можно использовать следующее правило, его называют «правило креста»: записывается равенство произведений элементов (чисел или выражений) стоящих по диагонали
a∙d=b∙c
Как видите результат тот же.
Если три элемента пропорции известны, то мы всегда можем найти четвёртый.
Именно в этом суть пользы и необходимость пропорции при решении задач.
Давайте рассмотрим все варианты, где неизвестная величина х находится в «любом месте» пропорции, где a, b, c – числа:

![]()
Величина стоящая по диагонали от х записывается в знаменатель дроби, а известные величины стоящие по диагонали записываются в числитель, как произведение. Его запоминать не обязательно, вы и так всё верно вычислите, если усвоили основное правило пропорции.
Теперь главный вопрос, связанный с названием статьи. Когда пропорция спасает и где используется? Например:
1. Прежде всего это задачи на проценты. Мы рассматривали их в статьях "Задачи на проценты. Часть 1!" и "Задачи на проценты. Часть 2!".
2. Многие формулы заданы в виде пропорций:
> теорема синусов
> отношение элементов в треугольнике

> теорема тангенсов

> теорема Фалеса и другие.
3. В задачах по геометрии в условии часто задаётся отношение сторон (других элементов) или площадей, например 1:2, 2:3 и прочие.
4. Перевод единиц измерения, причём пропорция используется для перевода единиц как в одной мере, так и для перевода из одной меры в другую:
— часы в минуты (и наоборот).
— единицы объёма, площади.
— длины, например мили в километры (и наоборот).
— градусы в радианы (и наоборот).
здесь без составления пропорции не обойтись.
Ключевой момент в том, что нужно правильно установить соответствие, рассмотрим простые примеры:

Необходимо определить число, которое составляет 35% от 700.
В задачах на проценты за 100% принимается та величина, с которой сравниваем. Неизвестное число обозначим как х. Установим соответствие:
Можно сказать, что семисот тридцати пяти соответствует 100 процентов.
Иксу соответствует 35 процентов. Значит,
700 – 100%
х – 35 %
Решаем

Ответ: 245

Переведём 50 минут в часы.
Мы знаем, что одному часу соответствует 60 минут. Обозначим соответсвие - x часов это 50 минут. Значит
1 – 60
х – 50
Решаем:
То есть 50 минут это пять шестых часа.
Ответ: 5/6

Николай Петрович проехал 3 километра. Сколько это будет в милях (учесть, что 1 миля это 1,6 км)?
Известно, что 1 миля это 1,6 километра. Число миль, которые проехал Николай Петрович примем за х. Можем установить соответствие:
Одной миле соответствует 1,6 километра.
Икс миль это три километра.
1 – 1,6
х – 3

Ответ: 1,875 миль
Вы знаете, что для перевода градусов в радианы (и обратно) существуют формулы. Я их не записываю, так как запоминать их считаю излишним, и так вам в памяти приходится держать много информации. Вы всегда сможете перевести градусы в радианы (и обратно), если воспользуетесь пропорцией.
Переведём 65 градусов в радианную меру.
Главное это запомнить, что 180 градусов это Пи радиан.
Обозначим искомую величину как х. Устанавливаем соответствие.
Ста восьмидесяти градусам соответствует Пи радиан.
Шестидесяти пяти градусам соответствует х радиан.

Если записать отношение в общем виде, то получится

То есть, если необходимо перевести градусы в радианы, то подставляете в эту пропорцию градусы и вычисляете радианы; если необходимо перевести радианы в градусы, то подставляете радианы и вычисляете градусы.
Можете изучить статью по этой теме на блоге. Материал в ней изложен несколько по иному, но принцип тот же. На этом закончу. Обязательно будет ещё что-нибудь интересненькое, не пропустите!
Если вспомнить само определение математики, то в нём есть такие слова: математика изучает количественные ОТНОШЕНИЯ (ОТНОШЕНИЯ — здесь ключевое слово). Как видите в самом определении математики заложена пропорция. Вообщем, математика без пропорции это не математика!!!
Всего доброго!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.








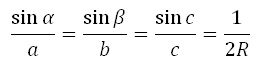
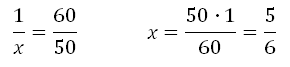








Спасибо за Ваши статьи! Моим ученикам они понравились тем, что излагаете все понятно и доступно!
Очень рад!
замечательно, спасибо!
Как решается такая задача: В субботу Руслан прочитал 30% книги, в воскресенье 75% остатка. Сколько страниц в книге, если в воскресенье он прочитал 126 страниц.
Наталья, здравствуйте! Задача простая, но «путанная».
Рассуждаем логически:
Все страницы берём за х.
Значит в субботу прочитано 0,3х. Значит в воскресенье 0,7х (это остаток).
0,75 остатка это будет 0,75*0,7х. Сказано, что это 126 страниц.
Получаем уравнение 0,75*0,7х=126
Ответ: 240
удачи!
Спасибо большое!!! Очень полезная статья. Здесь очень все понятно и удобно. По больше бы таких сайтов)
Помогитесли решить задачку,
За 12 часов 6 рабочих сделали 960 деталей, сколько рабочих сделают 4200 деталей за 35 часов.
Ответ должен быть 9, но я не могу понять как?
Добавил задачу сюда matematikalegko.ru/rabota...otu-chast-2.html
конечно 9 , вы правы.
Математику только за тем учить и следует) потому что ОНА ум у порядок приводит!