Сравнение дробей. В этой статье разберём различные способы используя которые можно сравнить две дроби. Рекомендую посмотреть весь список публикаций по дробям и изучать последовательно.
Прежде чем показать стандартный алгоритм сравнения дробей давайте разберём некоторые случаи, в которых сразу глядя на пример можно сказать которая из дробей будет больше. Здесь нет особой сложности, немного аналитики и всё готово. Посмотрите на следующие дроби:
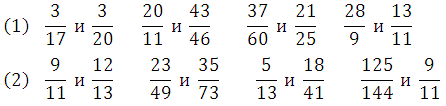
В строке (1) сразу можно определить какая дробь больше, в строке (2) это сделать затруднительно и тут применим «стандартный» (или его можно назвать наиболее часто применяемым) подход для сравнения.
Способ первый – аналитический.
1. Перед нами две дроби:
Числители равны, знаменатели неравны. Какая из них больше? Ответ очевиден! Больше та, у которой меньше знаменатель, то есть три семнадцатых. Почему? Простой вопрос: Что больше – одна десятая часть от чего либо или одна тысячная? Конечно же, одна десятая.
Получается, что при равных числителях больше та дробь, у которой меньше знаменатель. Не имеет значения стоят ли в числителях единицы или другие равные числа, суть не меняется.
Дополнительно к этому можно добавить следующий пример:
Какая из данных дробей больше (х положительное число)?
На основании уже представленной информации не трудно сделать вывод.
*Знаменатель первой дроби меньше, значит она больше.
2. Теперь рассмотрим вариант когда в одной из дробей числитель больше знаменателя. Пример:
Понятно, что первая дробь больше единицы, так как числитель больше знаменателя. А вторая дробь меньше единицы, поэтому без вычислений и преобразований можем записать:
3. При сравнении некоторых обыкновенных неправильных дробей явно видно, что у одной из них целая часть больше. Например:
В первой дроби целая часть равна трём, а во второй единице, поэтому:
4. В некоторых примерах также явно видно какая дробь больше, например:
Видно, что первая дробь меньше 0,5. Почему? Если выразить подробно, то:
а вторая больше 0,5:
Поэтому можно ставить знак сравнения:
Способ второй. «Стандартный» алгоритм сравнения.
Правило! Чтобы сравнить две дроби, необходимо чтобы знаменатели были равны. Тогда сравнение осуществляется по числителям. Больше будет та дробь, у которой больше числитель.
Пример:
*Это и есть основное ВАЖНОЕ ПРАВИЛО, которым пользуются для сравнения дробей.
Если даны две дроби с неравными знаменателями, то необходимо их привести к такому виду, чтобы они были равны. Для этого используется основное свойство дроби.
Сравним следующие дроби (знаменатели неравны):
Приведём их:
Как привести дроби к равным знаменателям? Очень просто! Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой.
Ещё примеры:
Обратите внимание, что знаменатель вычислять не обязательно (видно что они равны), для сравнения достаточно вычислить только числители.
*Все дроби, которые мы рассмотрели выше (первый способ) можно сравнить также используя этот подход.
На этом можно было бы закончить … Но есть ещё один «беспроигрышный» способ сравнения.
Способ третий. Деление столбиком.
Посмотрите пример:
Согласитесь, что для того чтобы привести к общему знаменателю и затем сравнить числители необходимо выполнить относительно объёмные вычисления. Используем следующий подход — выполним деление столбиком:
Как только мы обнаруживаем разницу в результате, то процесс деления можно остановить.
Вывод: так как 0,12 больше чем 0,11, то вторая дробь будет больше. Таким образом, можно поступать со всеми дробями.
На этом всё.
С уважением, Александр.
Делитесь информацией в социальных сетях.
