![]()
Найдите площадь параллелограмма. Здравствуйте! В этой статье представлена группа заданий решение которых связанно с площадью параллелограмма. Задачи входят в состав экзамена. Рекомендую посмотреть статью в которой о площади параллелограмма (и треугольника) всё подробно расписано. При решении пригодятся формулы:
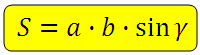
*Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
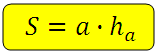
*Площадь параллелограмма равна произведению параллелограмма на высоту проведённую к этой стороне.
Также рассматриваются задачи с ромбами. Как известно, ромб является параллелограммом и обладает его свойствами, но есть ещё и дополнительные. Нам понадобится это:
— Диагонали ромба взаимно перпендикулярны.
Рассмотрим задачи:

27586. Найдите площадь ромба, если его стороны равны 1, а один из углов равен 1500.
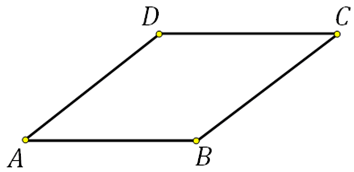
Используем формулу площади параллелограмма:
![]()
Стороны равны 1, а острый угол будет равен 300:
![]()
Ответ: 0,5

27614. Найдите площадь ромба, если его диагонали равны 4 и 12.
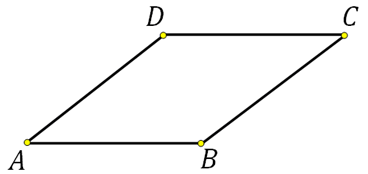
Известно, что диагонали ромба пересекаются под прямым углом, также они точкой пересечения делятся пополам. Построим эскиз следующим образом и отметим на нём размеры половин диагоналей:
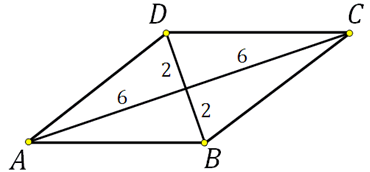
Получается, что ромб диагоналями разбивается на 4 равных прямоугольных треугольника с катетами 2 и 6. Можем вычислить площадь этого треугольника:
![]()
Так как все четыре треугольника образованные диагоналями равны, то
![]()
Ответ: 24

317338. Площадь параллелограмма ABCD равна 189. Точка Е середина стороны AD. Найдите площадь трапеции AECB.
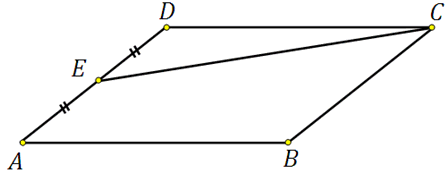
Для того чтобы вычислить площадь трапеции достаточно понимать как определить площадь отсечённого треугольника EDC. *Далее мы из площади параллелограмма просто вычтем площадь треугольника.
Посмотрите! Сторона треугольника ED равна половине стороны параллелограмма, высота у них общая. Что это значит? А то что:
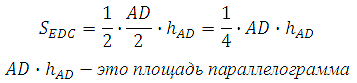
Получается, что площадь треугольника в четыре раза меньше площади параллелограмма:
![]()
Таким образом:
![]()
Ответ: 141,75
*Какую часть по площади занимает треугольник в параллелограмме можно увидеть разделив параллелограмм диагональю (он делится пополам):
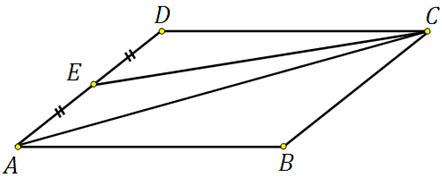
Площадь треугольника ADC составляет ½ от площади параллелограмма, а площадь треугольника EDC равна половине площади ADC, то есть треугольник EDC по площади будет в 4 раза меньше.

319056. Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A′B′C′D′, вершинами которого являются середины сторон данного параллелограмма.
Построим эскиз:
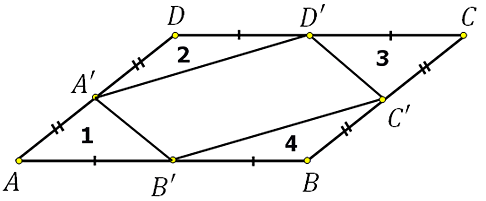
Нетрудно заметить, что площади треугольников 1, 2, 3 и 4 равны, так как у них есть равные стороны и синусы углов между ними приобретают равные значения.
Вычислим площадь треугольника АA′D′:
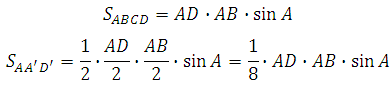
Получается, что площадь треугольника будет в восемь раз меньше. Таким образом, искомая площадь равна:
![]()
Ответ: 76,5
*Конечно же, «опытный глаз» сразу увидит, что площадь параллелограмма A′B′C′D′ в два раза меньше площади данного параллелограмма, но понимать формальное соотношение площадей фигур необходимо и важно.
**Если вы построите отрезки соединяющие середины противоположных сторон, то сразу наглядно увидите каким образом параллелограмм разбивается на равные по площади треугольники и решение будет очевидно.
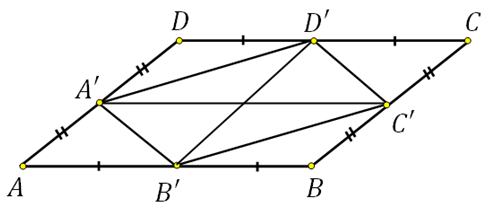

319057. Площадь параллелограмма ABCD равна 176. Точка E– середина стороны CD. Найдите площадь треугольника ADE.
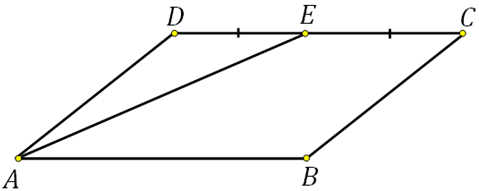
Площадь треугольника ADE составляет четвёртую часть от площади параллелограмма, посмотрите вше задачу 317338. То есть SADE=176/4=44.
Ответ: 44
![]()
27585. Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 300.
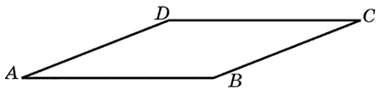
Посмотреть решение
27610. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
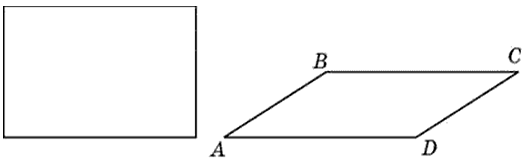
Посмотреть решение
27611. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
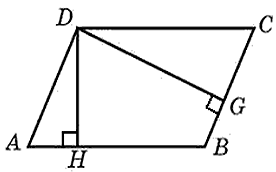
Посмотреть решение
27612. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Посмотреть решение
27613. Найдите площадь ромба, если его высота равна 2, а острый угол 300.
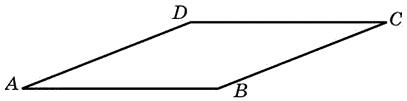
Посмотреть решение
27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.

Посмотреть решение
27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр
Делитесь информацией о сайте в социальных сетях.















