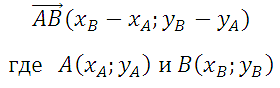Вычислить угол между векторами. В этой публикации хочу вам показать один способ определения угла между двумя векторами. В условии для каждого из векторов задаются координаты начала и конца. Векторы могут быть построены на координатной плоскости или без того. Конечно же, данную задачу обычно (и это естественно) решают применяя формулу скалярного произведения векторов, и такой подход был показан в этой статье.
Но если пофантазировать и представить, что вдруг вы напрочь забыли эту формулу или вообще в решении задач с векторами как-то давно не практиковались, то на помощь может прийти нижеизложенный способ. Это вполне достойная альтернатива. Чем у вас будет больше «инструментов» в запасе, тем лучше.

Найти угол между векторами. Ответ дать в градусах.