![]()
Здесь мы с вами рассмотрим некоторые задачи на проценты. Они несколько отличаются от задач изложенных ранее (Задачи 1), но никакой особой сложности не представляют. Что такое часть от числа, процент от числа можно вспомнить здесь. Напоню главное важное правило:

Теперь давайте выведем простые формулы. Учить их не нужно, необходимо просто понять.
Как вы уже знаете, если мы увеличиваем число х, например, на 20%, то записать это можно следующим образом:
 Теперь давайте увеличим число x на p процентов, получим формулу вида:
Теперь давайте увеличим число x на p процентов, получим формулу вида:
![]() Действительно, при раскрытии скобки получаем:
Действительно, при раскрытии скобки получаем:
![]() То есть числу х прибавляем часть от него которая соответствует р процентам.
То есть числу х прибавляем часть от него которая соответствует р процентам.
Аналогично, если величину х уменьшить на р процентов, то получим:
![]() Теперь внимание! Если величину х увеличить на р процентов, а затем полученную величину ещё раз увеличить на p процентов, то получим соответственно:
Теперь внимание! Если величину х увеличить на р процентов, а затем полученную величину ещё раз увеличить на p процентов, то получим соответственно:
 Если величину х уменьшить на р процентов, а затем полученную величину ещё раз уменьшить на p процентов, то получим соответственно:
Если величину х уменьшить на р процентов, а затем полученную величину ещё раз уменьшить на p процентов, то получим соответственно:
 Если величину х увеличить на р процентов, а затем на q процентов, получим соответственно:
Если величину х увеличить на р процентов, а затем на q процентов, получим соответственно:
![]() Если величину х уменьшить на р процентов, а затем на q процентов, получим соответственно:
Если величину х уменьшить на р процентов, а затем на q процентов, получим соответственно:
 Если величину х увеличить на р процентов, а затем уменьшить на q процентов, получим соответственно:
Если величину х увеличить на р процентов, а затем уменьшить на q процентов, получим соответственно:![]()
Если величину х уменьшить на р процентов, а затем увеличить на q процентов, получим соответственно:
Важно именно понимать эти формулы. Вы всегда сможете их легко восстановить в памяти или просто вывести при решении.
Рассмотрим задачи:

В 2010 году в городском квартале проживало 50000 человек. В 2011 году, в результате строительства новых домов, число жителей выросло на 15%, а в 2012 году — на 10% по сравнению с 2011 годом. Сколько человек стало проживать в квартале в 2012 году?
По условию, в 2011 году число жителей выросло на 15%, то есть их стало

Можно, конечно же, найти 15% от 50000 путём составления пропорции, и затем прибавить полученное число к 50000. Результат будет тот же.
А в 2012 году число жителей выросло на 10%, теперь уже по сравнению с 2011 годом. Получаем, что в 2012 году в квартале стало проживать

Или сразу можно было рассудить так: так как сначала число жителей увеличилось на 15%, а потом ещё на 10% от полученного, то можно было решать:

Ответ: 63250
Решить самостоятельно:


Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20700 рублей, через два года был продан за 16767 рублей.
Эта задача тоже решается по одной из формул, приведенных в начале. Холодильник стоил 20700 рублей. Его цена два раза уменьшилась на р%, и стала 16767. Значит,

Решаем квадратное уравнение:

Понятно, что реальный смысл имеет только ответ 10% (холодильник не может уменьшаться в цене на 190%).
Таким образом, цена холодильнтка уменьшалась на 10% каждый год.
Ответ: 10
Решить самостоятельно:


Митя, Антон, Гоша и Борис учредили компанию с уставным капиталом 200000 рублей. Митя внес 18% уставного капитала, Антон — 60000 рублей, Гоша — 0,18 уставного капитала, а оставшуюся часть капитала внес Борис. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1100000 рублей причитается Борису? Ответ дайте в рублях.
Выразим все доли соучредителей в процентах.
Митя внёс 18%.
Антон внёс 60000 рублей. Составим пропорцию и найдём какой он внёс процент:
200000 руб – 100%
60000 руб – x%

Гоша внёс 0,18 – это 18%.
Борис внёс остальное: 100–18–30–18 = 34%
Какой бы прибыль не была, но если она делится пропорционально внесённому вкладу, это означает, что каждый получает свой изначально внесённый процент от прибыли (или часть, сути это не меняет).
У нас в задаче 1100000 рублей прибыли.
Борис должен получить от неё 34% (или 0,34).
Значит, Борису причитается 0,34∙1100000 = 374000 рублей.
Ответ: 374000
Решить самостоятельно:

По процессу решения следующих задач можно сказать следующее: далеко не всегда в задачах на проценты нужно стремиться к нахождению неизвестной величины, которую мы обозначаем за х (стоимость, зарплата и прочее) порой это и невозможно сделать. Иногда в задачах требуется грамотно сопоставить данные из условия, правильно составить уравнение или систему уравнений, и провести необходимые преобразования.

В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 9% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
На первый взгляд, кажется, что цена акций вообще не должна измениться. Ведь они подорожали и подешевели на одно и то же число процентов! Но это впечатление ложное.
Пусть при открытии торгов в понедельник акции стоили х рублей. К вечеру понедельника они подорожали на р% и стали стоить х(1 + р/100).
Теперь уже эта величина принимается за 100%, и к вечеру вторника акции подешевели на р% по сравнению этой величиной. Соберем данные в таблицу:

По условию, акции в итоге подешевели на 9%, значит стали стоить

Получаем, что
 Поделим обе части уравнения на х (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения (разность квадратов):
Поделим обе части уравнения на х (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения (разность квадратов):

По смыслу задачи р > 0. Получаем, что р = 30.
Акции кампании в понедельник подорожали на 30%.
То есть, изначально стремиться к нахождению самой стоимости акций не нужно.
Ответ: 30
Решите самостоятельно:


Пять рубашек дешевле куртки на 15%. На сколько процентов восемь рубашек дороже куртки?
Так как нам неизвестна ни стоимость рубашки, ни стоимость куртки, то примем стоимость рубашки за х, стоимость куртки за у. Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки.
Значит стоимость пяти рубашек составляет 85% от цены куртки, то есть 5х = 0,85у. Для того, чтобы определить стоимость восьми рубашек необходимо найти стоимость одной, она будет в 5 раз меньше:

Таким образом, стоимость восьми рубашек равна:

Получили, что восемь рубашек на 36% дороже куртки.
Как видите, в данной задаче стремится к нахождению стоимости рубашки и куртки не нужно.
Ответ: 36
Решить самостоятельно:


Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась втрое, общий доход семьи вырос бы на 120%. Если бы стипендия дочери уменьшилась в 4 раза, общий доход семьи сократился бы на 6%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Так как нет никаких данных о конкретной зарплате каждого (в рублях) принимаем х – зарабатывает муж, у – жена, z – дочь.
Составим таблицу. Ситуации, о которых говорится в задаче («если бы зарплата мужа увеличилась, если бы стипендия дочки уменьшилась...») назовем «А» и «В».

Когда в условии задачи речь идёт о каких-то двух (и более) вариантах, то это обычно означает, что мы можем составить уравнения (это касается и задач на растворы в том числе). В данном случае можем составить два уравнения.
Сказано: если бы зарплата мужа увеличилась втрое, общий доход семьи вырос бы на 120%, первое уравнение
![]()
Сказано: если бы стипендия дочери уменьшилась в 4 раза, общий доход семьи сократился бы на 6%, второе уравнение
![]()
Система:

Мы видим два уравнения и три неизвестных!
Когда даны два уравнения с тремя неизвестными мы не сможем найти x, y, z по отдельности. Нам это и не нужно.
Возьмем первое уравнение и из обеих его частей вычтем сумму x + y + z.
Получим: 2х = 1,2 (x + y + z), то есть х = 0,6 (x + y + z)
А это значит, что зарплата мужа составляет 60% от общего дохода семьи.
Во втором уравнении мы также вычтем из обеих частей выражение
 Получаем:
Получаем:
Значит стипендия дочки составляет 8% от общего дохода семьи.
Таким образом, зарплата жены составляет 100 – 60 – 8 = 32 процента от общего дохода семьи.
*В задачах, где описываются 2 и более «ситуации» следует составлять уравнения и решать их систему. Этот подход также применяется в задачах на смеси.
Второй подход.
Обозначим х – это часть дохода (в процентах), который зарабатывает муж, у – жена, z –дочь. Учитывая данные в условии, можем записать:
 Находим разность первого и второго уравнения, получим:
Находим разность первого и второго уравнения, получим:

То есть зарплата мужа составляет 60 процентов от общего дохода.
Теперь вычислим разность первого и третьего уравнения: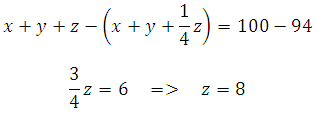 Это процент от дохода семьи, который приносит дочь. Остаётся вычислить какой процент составляет зарплата жены: 100 – 60 – 8 = 32
Это процент от дохода семьи, который приносит дочь. Остаётся вычислить какой процент составляет зарплата жены: 100 – 60 – 8 = 32
Ответ: 32
Решить самостоятельно:

На этом закончим. В данной рубрике продолжим рассматривать задачи, не пропустите! Всего наилучшего. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
















Александр,разве такие задачи вообще есть в банке заданий?Они,конечно,требуют внимания,но будут ли подобные задачи на ЕГЭ?
Александр,по моим подсчетам я получил число 1799.01
Правильно?
Нет 😉
Ответ: 1799.
Павел, верно. Жду телефон на email. С уважением!!!
Александр,когда ожидать сложную задачку с пауком в лабиринте?
Скоро, совсем скоро.