![]()
Значения тригонометрических функций. Друзья, прошлой статье, при рассмотрении тригонометрических уравнений, я пообещал вам привести алгоритм быстрого «восстановления» значений тригонометрических функций от 0 до 90 градусов. Решил далеко не откладывать, будущее уже настало )). Если хотите скачать данную теорию в pdf формате, подпишитесь на рассылку (в МЕНЮ вкладка ПОДАРКИ). Вы получите все прототипы задач базовой части с ответами и теорию систематизированную по группам задач от 1 до 14.
Предлагаю вам алгоритм, благодаря которому вы легко, в течение минуты восстановите в памяти все вышеуказанные значения:
1. Записываем в строчку углы от 0 до 90 градусов. Слева в столбик запишем сначала синус, затем косинус аргумента:
2. Напротив синуса пишем числа от нуля до четырёх (под значениями углов). Напротив косинуса от 4 до 0:
3. Далее извлекаем корень:
4. Делим на 2:
5. Вычисляем:
Мы получили значения синуса и косинуса углов от 0 до 90 градусов. Далее, зная формулы тангенса и котангенса:
вы сможете найти значения для указанных углов.
И так для тангенса и котангенса любого угла. Данная шпаргалка представленная выше может выручить.
*Конечно, к пониманию того, каким значениям равны тригонометрические функции различных углов (имею виду углы 0, 30, 45, 60, 90, 120 и так далее), какие ставить знаки при этих значениях лучше прийти через понимание тригонометрической окружности.
Кстати, вы можете расширить диапазон углов и записать углы от 0 до 180 градусов, но тогда напротив синуса и косинуса нужно будет поставить числа в следующем порядке:
Далее выполняем те же действия, учитывая один нюанс: корень в строке с косинусом извлекаем из положительного числа, минус ставим перед корнем:
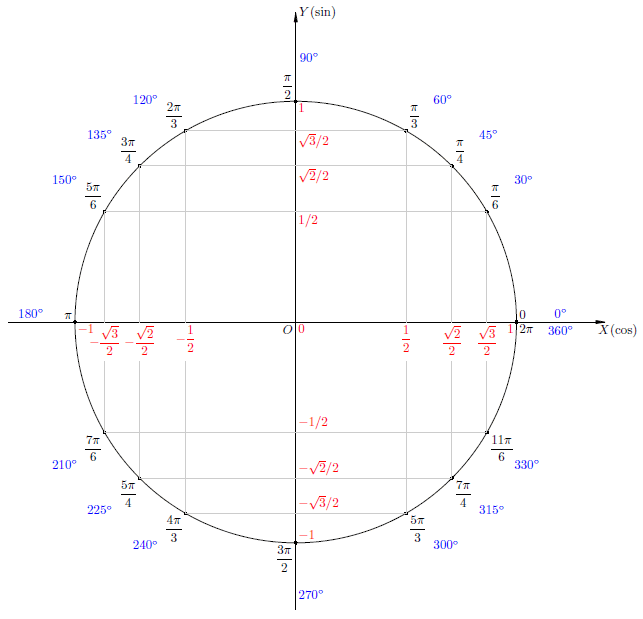
Тригонометрическая окружность
Описывать подробно, как определять значения функций, которые соответствуют определённому углу здесь не буду, сделаю это в одной из будущих статей, не пропустите!
Объясню лишь принцип: косинус угла – это абсцисса точки на тригонометрической окружности, которая соответствует данному углу; синус угла – это ордината точки на тригонометрической окружности, которая соответствует данному углу.
Например по представленному рисунку видно, что косинус нуля градусов равен 1, косинус 120 градусов равен минус 0,5 и так далее, надеюсь, логику вы уловили.
Спасибо за внимание, учитесь с удовольствием!
С уважением, Александр крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.








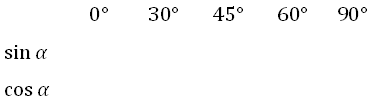
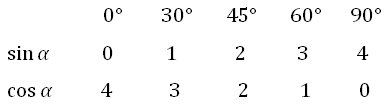
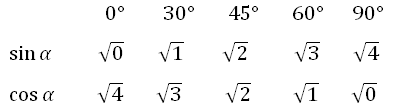

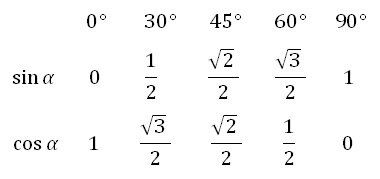

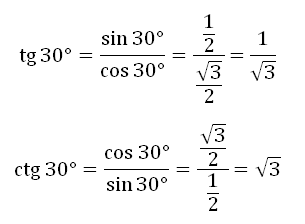
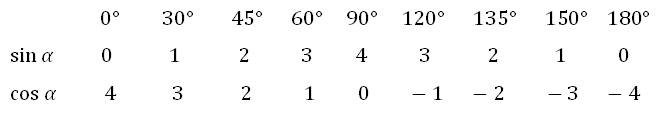








Считаю предложенную методику запоминания вредной. Методика не может быть целью. Запоминание должно быть произвольным и мотивированным.
Это школьником можно так манипулировать.
Попробуйте обучать такими методиками военных пилотов!
Знание должно быть понятым, осознанным и готовым к применению как оружие.
Такой псевдодидактический подход к обучению ведет к деградации как математического образования, так и ученика и учителя.
Спасибо, что выразили своё мнение. Какой путь вы считаете правильным для запоминания значений указанных углов и какой способ можете предложить быстрого восстановления этой информации?
Конечно, то как дают этот материал в 8 классе
interneturok.ru/ru/school...0&chapter_id=938
считаю верным, значения выводятся через понимание основ.
Но вы представляете, что будет происходить на уроке, если ученик подобным образом будет «вспоминать» эти значения?
Как правило ребятам предлагается механическое заучивание этих значений, чтоб от зубов отскакивало. И в дальнейшем ученик не теряет время при решении.
Если бы вы внимательно прочитали статью, то увидели бы, что этот способ не предлагается в виде доктрины и ЗАКОНА, а только лишь как метод, как вариант. И многим это помогает. Чем больше «инструментов» в арсенале, тем лучше.
Очень полезная и интересная информация! Спасибо! Попробую научить этому ребенка. Если получится, то есть надежда, что потом ребенок сам будет пытаться найти во всем какую-то систему для запоминания.