![]()
Здравствуйте, Дорогие друзья! Задачи по геометрии повышеyной сложности довольно разнообразны. Для решения данных задач необходимо обладать хорошими теоретическими знаниями и практическими навыками. Какими? Подробно будет изложено в одной из будущих статей, не пропустите! Здесь мы рассмотрим задачу.

В прямоугольном параллелепипеде ADCDA1B1C1D1 заданы длины ребер AD = 12, AB = 5, AA1 = 8. Найдите объем пирамиды MB1C1D, если M — точка на ребре AA1, причем AM = 5.
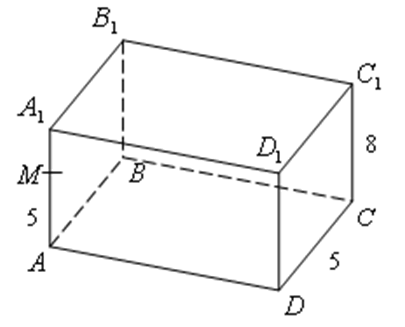
Решение:
Какова сложность в данной задаче? Дело в том, что не все могут представить — как расположена пирамида. Понятно, что B1C1D это основание пирамиды, а как «увидеть» и построить её высоту — непонятно.
Запишем формулу объёма пирамиды:

Предлагаю поступить следующим образом. Найдём объём пирамиды MAB1C1D. Её объём будет в два раза больше объёма пирамиды MB1C1D, так как основание AB1C1D в два раза больше чем B1C1D. Пирамиду MAB1C1D представить проще, а также проиллюстрировать её высоту.
Построим пирамиду:

Вычисляем площадь AB1C1D:
![]()
Найдём высоту. Высотой пирамиды MAB1C1D является перпендикуляр, опущенный из точки М к AB1. Обозначим точку Е (точка пересечения) :

Нам известны: AB = 5, MA = 5 BB1 = 8.
Треугольник AME подобен треугольнику B1AB.
Значит,

Как ещё можно найти МЕ?
Из треугольника AA1B1 можем найти:

Теперь рассмотрим треугольник AME:

Как видите результат тот же.
То есть мы нашли высоту пирамиды MAB1C1D (она же является высотой пирамиды MB1C1D, она у них общая).
Вычисляем объём MAB1C1D:

Как уже было сказано, объём пирамиды MB1C1D в два раза меньше объёма пирамиды MAB1C1D, то есть искомый объём равен 50.
Ответ: 50
Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.















