![]()
Прямоугольник. Задачи. Продолжаем рассматривать задания ЕГЭ. В этой заметке рассмотрим примеры с прямоугольниками и квадратами. Решения просты, вопросы связаны нахождением сторон, периметра, диагонали, углов. Необходимо знать свойства этих фигур, также в ходе решения может использоваться квадратное уравнение. Рассмотрим задачи:

27601. Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.

Площадь прямоугольника равна произведению его соседних сторон. Обозначим AD как х, тогда DC будет равно х+3. Можем записать:

Решив квадратное уравнение получим кони 3 и –6.
*Так как в условии числа небольшие, то можно обойтись без вычислений и решить её просто методом перебора: стороны могут быть равны 1 и 4, 2 и 5, 3 и 6. Сразу видно, что условию отвечает пара 3 и 6. То есть задачка решается за 10 секунд.
Ответ: 6

27603. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1 : 2.

Соседние стороны соотносятся как 1 к 2, введём коэффициент пропорциональности х и выразим площадь, получим:

Значит дна сторона равна 3, другая в два раза больше, то есть 6. Периметр будет равен 3+6+3+6=18.
Ответ: 18

27606. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.

Обозначим AD=x, AB=y. Периметр равен:

Площадь равна:
![]()
Имеем два уравнения, можем составить систему:

Выразим x во втором уравнении и подставим в первое:


Решая квадратное уравнение:

Значит

Получили, что то стороны равны 5 и 12. По теореме Пифагора вычислим диагональ:
![]()
Второй способ:
Обратите внимание! Диагональ у нас равна:
![]()
Имеем
![]()
Преобразуем первое:

Следовательно:

Ответ: 13

27810. Меньшая сторона прямоугольника равна 6, диагонали пересекаются под углом 600. Найдите диагонали прямоугольника.

Вычисляется устно. Так как диагонали пересекаются по углом 600, то треугольники ADO и COB будут являться равносторонними, кроме этого они равны. Значит AD=DO=OB=3, следовательно диагональ равна 6.
Ответ: 6
27811. Найдите диагональ прямоугольника, две стороны которого равны 6 и 8.

По теореме Пифагора:
![]()
Ответ: 10

27812. Диагональ прямоугольника вдвое больше одной из его сторон. Найдите больший из углов, которые образует диагональ со сторонами прямоугольника? Ответ выразите в градусах.

Рассмотрим прямоугольный треугольник ACB. Известно, что катет лежащий против угла 30 градусов равен половине гипотенузы. У нас по условию AD равно половине AB, следовательно угол DCB равен 300.
Таким образом, искомый угол равен 600.
Ответ: 60

27813. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 6. Найдите диагональ данного прямоугольника.

Так как диагональ делит угол в отношении 1 к 2, то можем сделать вывод о том, что углы эти будут равны 300 и 600 (один в два раза больше другого).
Рассмотрим прямоугольный треугольник ADC. Известно, что катет лежащий против угла 300 равен половине гипотенузы. Катет этот равен, то есть AD=6. Следовательно АС=12.
Ответ: 12

27814. Найдите сторону квадрата, диагональ которого равна √8.

Пусть сторона квадрата равна а. По теореме Пифагора:

Ответ: 2

27815. В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 7. Найдите периметр этого квадрата.

Расстояние от точки пересечения диагоналей до стороны равно половине стороны, значит сторона будет равна 14. Таким образом периметр равен 14∙4=56.
Ответ: 56

27830. Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 24.
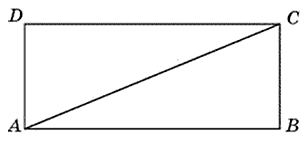
Пусть одна сторона равна а, другая b. Выразим периметр прямоугольника:
![]()
Выразим периметр треугольника:
![]()
Выразим в первом уравнении:
![]()
Подставим во второе, получим:

Это и есть диагональ. То есть нам совсем необязательно вычислять сами стороны.
Ответ: 10

27831. Середины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

*Понятно, что образовавшийся является ромбом.
Рассмотрим треугольник ADC. В нём HG является средней линией, так как H и G это середины сторон. Известно, что средняя линия треугольника равна половине параллельного ему основания, то есть HG=2,5.
Значит периметр будет равен 4∙2,5=10.
Ответ: 10

27832. В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 1 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника.

Пусть OG=х, тогда OH=х+1. Тогда

Таким образом
![]()
Ответ: 6

27947. Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1.

Центр описанной окружности лежит на середине диагоналей прямоугольника. По клеткам видно, что диагональ равна пяти. Следовательно радиус равен 2,5.
Ответ: 2,5

27948. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными √2.

Центр вписанной в квадрат окружности лежит на точке пересечения диагоналей. По рисунку видно, что радиус указанной окружности равен диагонали клетки. Сторона клетки равна корню из двух. По теореме Пифагора:

Ответ: 2
Решить самостоятельно:
27583. Найдите диагональ квадрата, если его площадь равна 2.
27584. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9.
27600. Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
27602. Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1 : 2.
27604. Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
27605. Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
27607. Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.
27608. Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.

27609. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?

27610. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Найдите сторону квадрата, описанного около окружности радиуса 4. Ответ: 8
На этом всё. Всего доброго!
С уважением, Александр Крутицких.















