Угол между прямыми в призме

Угол между прямыми в призме. Для вас очередной материал – мы рассмотрим пару задач с призмами. Требуется определить угол между прямыми проходящими через указанные вершины призмы. Дело в том, что эти прямые не лежат в одной плоскости. Такие прямые называют скрещивающимися.

Если вы с ними уже знакомы, то задачки решите сразу сходу после построения эскиза без всяких вычислений. Если нет, то посмотрите соответствующую теорию, можете посмотреть информацию здесь, материал подан достаточно наглядно.

Принцип прост – необходимо одну из прямых переместить до пересечения со второй параллельным переносом. Либо установить — имеется ли параллельная ей прямая в одной плоскости со второй прямой. Рассмотрим задачи:

316553. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра которой равны 8, найдите угол между прямыми FA и D₁Е₁. Ответ дайте в градусах.

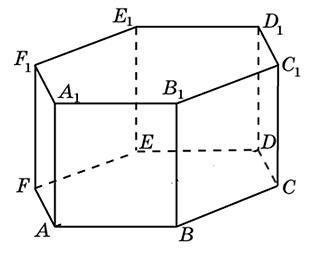
Построим прямые, переместим параллельным переносом прямую  D₁Е₁ до пересечения с прямой AF. Полученная прямая будет проходить через DE:

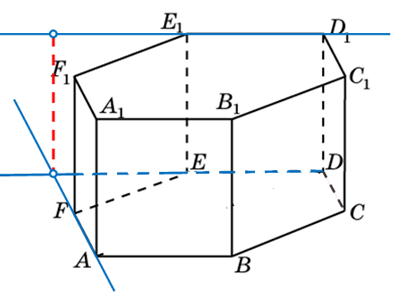
Зная свойства правильного шестиугольника, а именно, то что углы при его вершинах равны 120 градусам, мы уже можем записать ответ. Угол между указанными прямыми равен 60⁰. Если посмотреть на призму сверху, то эскиз будет выглядеть так:

*Как видим, на самом деле, чему равна длина ребра не имеет значения.

Ответ: 60

316558. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 3, найдите угол между прямыми AA₁и BC₁. Ответ дайте в градусах.

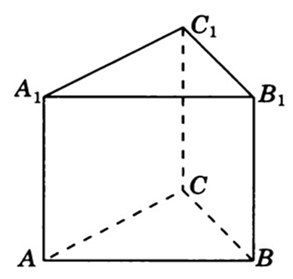
Построим указанные прямые и параллельным переносом «передвинем» прямую  AA₁ до грани  BCC₁B₁ через которую проходит BC₁:

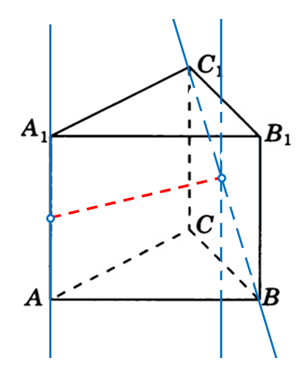
Так как в условии сказано, что все рёбра равны 3, то это значит что грань BCC₁B₁  является квадратом. Прямая BC₁ является диагональю этого квадрата и она пересекает все прямые параллельные боковым рёбрам под углом 45 градусов.  Наглядно это можно увидеть на проекции призмы:

*Небольшая оговорка. В обеих задачах мы перемещали прямые как бы «стягивая» их по соединяющему их перпендикуляру (обозначен красным пунктиром). Необязательно это делать именно так. Важно, чтобы одна из прямых была перемещена до пересечения с другой именно параллельным сдвигом. Во второй задаче это можно было сделать и так:

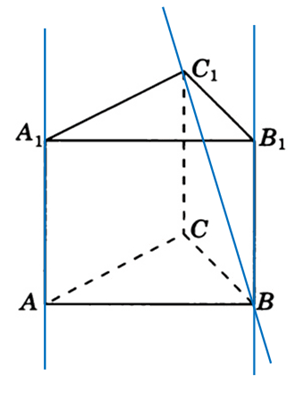
На этом закончим. Так что если встретите скрещивающиеся прямые на ЕГЭ в задаче кратким ответом, не пугайтесь, решаются они устно. Важно понимать, каким образом переместить прямую до пересечения с другой. А уж угол найти, как говорится, это дело техники.

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.