Одна из граней прямоугольного параллелепипеда

Предлагаю вашему вниманию ещё две задачи с параллелепипедами. На данный момент рассмотрены почти все задачи с кубами и параллелепипедами, которые присутствуют в открытом банке заданий ЕГЭ по математике. С ними вы можете ознакомиться, посмотрев предыдущие статьи. В представленных ниже задачах есть некоторые особенности. Что ж, приступим:

Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна 2 и образует с плоскостью этой грани угол 30⁰. Найдите объем параллелепипеда.

Построим данный параллелепипед. Сказано, что диагональ образует с гранью, являющейся квадратом угол в 30⁰, поэтому выполним построение следующим образом – грань в основании у нас будет являться квадратом, далее на этом основании строим сам параллелепипед, затем строим диагональ и обозначаем вершины:

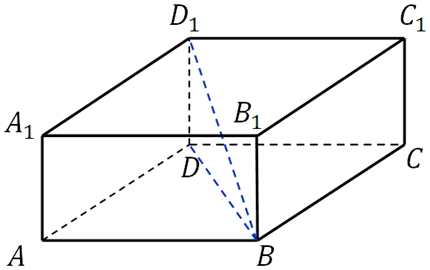
Угол между диагональю и основанием это угол DBD₁ в прямоугольном треугольнике  BD₁D, так как плоскость проходящая через точки  D, B и D₁ в данном параллелепипеде перпендикулярна плоскости основания.

Для того, чтобы найти объём параллелепипеда нам нужно знать три  его рёбра.

В прямоугольном треугольнике BD₁D мы можем найти DD₁, так как нам известна его гипотенуза и острый угол:

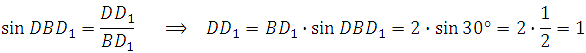
Для того, чтобы найти рёбра AB и AD,  достаточно знать чему равна диагональ BD квадрата ABCD.

Отрезок BD мы также можем найти из рассмотренного нами прямоугольного треугольника. По теореме Пифагора:

Теперь найдём АВ.  По теореме Пифагора:

Так как AB = AD, то

Значит

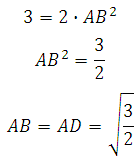
Теперь можем найти объём параллелепипеда:

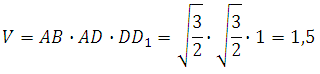
Ответ: 1,5

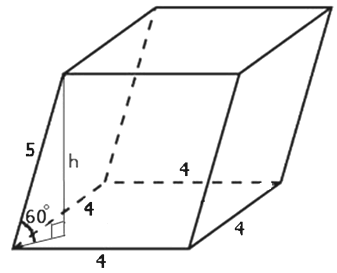
Гранью параллелепипеда является ромб со стороной 4 и острым углом 60⁰. Одно из ребер параллелепипеда составляет с плоскостью этой грани угол 60⁰ и равно 5. Найдите объем параллелепипеда.

*Условие данной задачи может некоторых немного «запутать», тем более, если не будет дан рисунок. Вроде как речь идёт об одной какой-то грани, которая является ромбом…

У кого-то может возникнуть  вопрос: а что с остальными гранями, чем они являются и как расположены?

Так же сказано, что одно из рёбер с плоскостью этой грани составляет угол 60⁰. Об остальных рёбрах вроде как и нет речи.

Здесь всё просто. Нужно помнить что представляет из себя параллелепипед – это тело, гранями которого являются параллелограммы.

Вернёмся к условию. Так как сказано, что одна из граней это ромб и одно из рёбер с данной гранью составляет угол 60⁰, то смело можете сразу эту грань принять как основание параллелепипеда, при чём все остальные рёбра будут расположены под тем же углом к основанию, что оговоренное в условии.

Условие задачи могло бы звучать так:

Основанием параллелепипеда является ромб со стороной 4 и острым углом 60⁰. Боковые рёбра параллелепипеда составляют с плоскостью этой грани угол 60⁰ и равны 5. Найдите объем параллелепипеда.

Строим сам параллелепипед:

Покажем на эскизе заданные размеры:

Объём параллелепипеда равен произведению площади его основания и высоты:

S – площадь основания параллелепипеда

h – высота параллелепипеда

Площадь ромба (основание параллелепипеда) с острым углом в 60° равна двум площадям равносторонних треугольников:

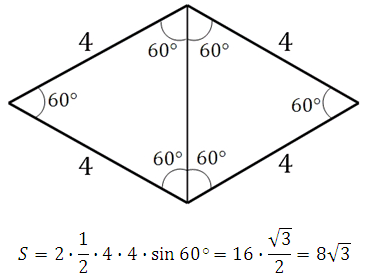
*Использовали  формулу:  площадь треугольника равна половине произведения соседних сторон на синус угла межу ними.

Высоту можем найти из прямоугольного треугольника, в котором нам известна гипотенуза равная пяти и острый угол  60⁰. По определению синуса в прямоугольном треугольнике:

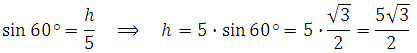
 Вычисляем объем:

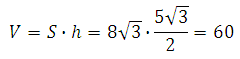
Ответ: 60

27103. Диагональ прямоугольного параллелепипеда равна корню из восьми и образует углы 30⁰, 30⁰ и 45⁰ с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

Посмотреть решение

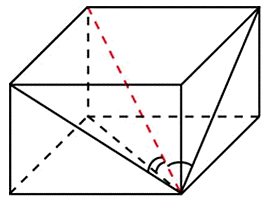
27104. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60⁰. Одно из ребер параллелепипеда составляет с этой гранью угол в 60⁰ и равно 2. Найдите объем параллелепипеда.

Посмотреть решение

В будущем продолжим рассматривать задачи по стереометрии, не пропустите!

На этом всё! Успеха вам!

С уважением, Александр

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.