![]()
Ещё пару задачек связанных с параллелепипедами. Данные задания от остальных, рассмотренных ранее, отличаются тем, что здесь требуется найти площадь сечения.
Сами вычисления минимальны. Основная трудность у некоторых может возникнуть именно в построении самого сечения. Что ж, все рекомендации даны ниже, приступим:

315131. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB = 2, ребро AD равно корню из пяти, ребро AA1 = 2. Точка K — середина ребра BB1. Найдите площадь сечения, проходящего через точки A1, D1 и K.
Построим параллелепипед, обозначим вершины и точку К. Затем построим плоскость, проходящую через точки A1, D1 и K:

Сечением является прямоугольник с соседними сторонами A1D1 и A1K (обозначен синим контуром). Для того, чтобы найти его площадь необходимо знать отрезок A1K.
Отрезок A1D1 = AD, так как параллельные рёбра у параллелепипеда равны:
![]()
Найдём A1K. По теореме Пифагора:
Значит
![]()
Таким образом, можем найти площадь сечения:
![]()
*Плоскость сечения обычно задаётся тремя точками, поэтому есть «соблазн» по данным трём точкам построить треугольник и найти его площадь. Совет: мысленно представьте, что как будто бы вы делаете срез ножом. Запомните, что у фигуры, которая является сечением, все её стороны должны лежать на гранях и рёбрах заданного тела.
**И ещё. Если в прямоугольном параллелепипеде плоскость проходит через любое его ребро и рассекает этот параллелепипед, то сечением всегда будет являться прямоугольник.
Ответ: 5

316552. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB = 24, AD = 10, AA1 = 22. Найдите площадь сечения, проходящего через вершины A1, A1 и C.
Построим параллелепипед, обозначим вершины. Затем построим плоскость, проходящую через точки A1, А1 и С:

Сечением является прямоугольник (обозначен синим цветом). Для того, чтобы найти его площадь необходимо найти АС. Ребро AA1 нам известно.
По теореме Пифагора:
![]()
Таким образом, можем найти площадь сечения:
![]()
Ответ: 572
Ещё раз повторюсь: для того, чтобы задать плоскость достаточно три точки (и в задачах, обычно, она так и задаётся), но само сечение может проходить и через 4 и через 5 и более точек, лежащих на рёбрах тела ( такие тела как призмы, пирамиды, параллелепипеды).
Поэтому будьте внимательны при построении сечения. Кроме того, помните, что сечение это всегда плоская фигура!
*Конечно, существуют и другие способы задания сечений, но об этом не здесь.
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.








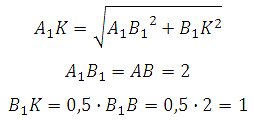








Спасибо за подборку задач с решениями.
Галина Михайловна, пожалуйста. Ещё будет одна с параллелепипедами, последняя.